Poisson's ratio proof

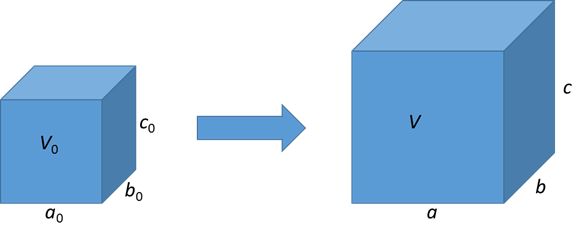
Consider the strained body above. In each orthogonal direction, we have

\[ a = \left( {1 + {\varepsilon_1}} \right){a_0} \]

\[ b = \left( {1 + {\varepsilon_2}} \right){b_0} \]

\[ c = \left( {1 + {\varepsilon_3}} \right){c_0} \]

The volume of the strain body is

\[ V = abc = \left( {1 + {\varepsilon_1}} \right)\left( {1 + {\varepsilon_2}} \right)\left( {1 + \varepsilon{_3}} \right){a_0}{b_0}{c_0} \]

The volumetric strain, or dilation is defined as

\[ {\rm{\Delta }} = \frac{{{\rm{\Delta }}V}}{{{V_0}}} = \frac{{abc - {a_0}{b_0}{c_0}}}{{{a_0}{b_0}{c_0}}} = \left( {1 + \varepsilon{_1}} \right)\left( {1 + {\varepsilon_2}} \right)\left( {1 + {\varepsilon_3}} \right) - 1 = {\varepsilon_1} + {\varepsilon_2} + {\varepsilon_3} + O\left( {{\varepsilon^2}} \right) \]

The higher order terms are negligible for small strains, which is indeed true if we want to consider the case for volume conservation.

Now using Poisson’s ratio for isotropic materials,

\[ {\varepsilon_2} = {\varepsilon_3} = - \nu {\varepsilon_1} \]

If volume is conserved,

\[ {\rm{\Delta }} = 0; {\varepsilon_1} + {\varepsilon_2} + {\varepsilon_3} = 0; \left( {1 - 2\nu } \right){\varepsilon_1} = 0 \]

We have Poisson’s ratio \( \nu = 0.5 \) for volume conservation.