The strain tensor

When stress is applied to the material, strain is produced. Strain is also a symmetric second-rank tensor. Stress and strain are related by:

σij = Cijklεkl

The strain tensor, εkl, is second-rank just like the stress tensor. The tensor that relates them, Cijkl, is called the stiffness tensor and is fourth-rank.

Alternatively:

εij= Sijklσkl

Sijkl is called the compliance tensor and is also fourth-rank.

The strain tensor is a field tensor – it depends on external factors. The compliance tensor is a matter tensor – it is a property of the material and does not change with external factors.

Expressing the strain in a slip process in terms of displacement

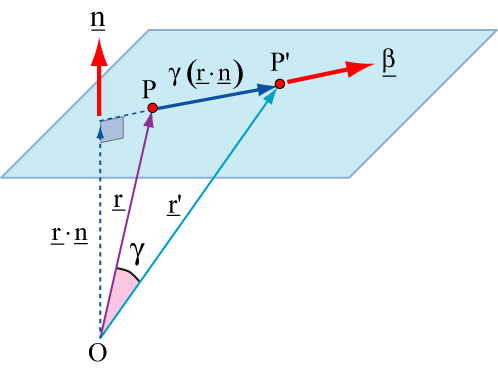
This diagram shows a plane on which slip occurs. A general point P is moved to position P' by the slip. The vectors from the origin to P and P' are r and r' respectively. Also shown is the unit vector n > normal to the plane, and β perpendicular to the plane from O. The length of the perpendicular from O to the plane is simply r·n. Unit vector n has components of n₁, n₂, n₃, and r has components of x₁, x₂, x₃.

Suppose the distance moved in the direction of slip is \(\gamma \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r} \cdot \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} } \right)\). The displacement vector that represents slip is then given by:

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r} ' - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r} = \gamma \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r} \cdot \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} } \right)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\beta } $$

where β is a unit vector in the direction of slip and has components of b₁, b₂ and b₃.

If the strain angle is small, the components of the deformation tensor eij can be obtained by differentiating the displacements, so that

$${e_{ij}} = {{\partial {u_i}} \over {\partial {x_j}}} = {\partial \over {\partial {x_j}}}\gamma \left( {{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r} \cdot \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} } } \right){\beta _i}$$

Hence, for example,

$${e_{11}} = {{\partial {u_1}} \over {\partial {x_1}}} = {\partial \over {\partial {x_1}}}\gamma \left( {{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r} \cdot \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{n} } } \right){\beta _1} = \gamma {\beta _1}{\partial \over {\partial {x_1}}}\left( {{x_1}{n_1} + {x_2}{n_2} + {x_3}{n_3}} \right) = \gamma {n_1}{\beta _1}$$

More generally,

$${e_{ij}} = {{\partial {u_i}} \over {\partial {x_j}}} = \gamma {n_j}{\beta _i}$$

We can then write the tensor like this:

$${e_{ij}} = \gamma \left( {\matrix{ {{n_1}{\beta _1}} & {{n_2}{\beta _1}} & {{n_3}{\beta _1}} \cr {{n_1}{\beta _2}} & {{n_2}{\beta _2}} & {{n_3}{\beta _2}} \cr {{n_1}{\beta _3}} & {{n_2}{\beta _3}} & {{n_3}{\beta _3}} \cr } } \right)$$ $${\varepsilon _{ij}} = \gamma \left( {\matrix{ {{n_1}{\beta _1}} & {{1 \over 2}\left( {{n_2}{\beta _1} + {n_1}{\beta _2}} \right)} & {{1 \over 2}\left( {{n_3}{\beta _1} + {n_1}{\beta _3}} \right)} \cr {{1 \over 2}\left( {{n_1}{\beta _2} + {n_2}{\beta _1}} \right)} & {{n_2}{\beta _2}} & {{1 \over 2}\left( {{n_3}{\beta _2} + {n_2}{\beta _3}} \right)} \cr {{1 \over 2}\left( {{n_1}{\beta _3} + {n_3}{\beta _1}} \right)} & {{1 \over 2}\left( {{n_2}{\beta _3} + {n_3}{\beta _2}} \right)} & {{n_3}{\beta _3}} \cr } } \right)$$

Separation of the strain tensor

Notice that the tensor derived from the diagram is e_ij while the strain tensor related to the stress tensor by the stiffness and compliance tensors is εij. This is not a mistake!

The tensor eij derived from the diagram describes the specimen moving relative to the origin. This includes a change in dimension of the specimen, the strain. It also may include a rotation of the specimen. In terms of the properties of the material, the rotation is not of interest, so we must separate it out to be left with the strain alone.

eij = εij + ωij

where εij is the strain tensor and ωij is the rotation tensor.

$${\omega _{ij}} = \gamma \left( {\matrix{ 0 & {{1 \over 2}\left( {{n_2}{\beta _1} - {n_1}{\beta _2}} \right)} & {{1 \over 2}\left( {{n_3}{\beta _1} - {n_1}{\beta _3}} \right)} \cr {{1 \over 2}\left( {{n_1}{\beta _2} - {n_2}{\beta _1}} \right)} & 0 & {{1 \over 2}\left( {{n_3}{\beta _2} - {n_2}{\beta _3}} \right)} \cr {{1 \over 2}\left( {{n_1}{\beta _3} - {n_3}{\beta _1}} \right)} & {{1 \over 2}\left( {{n_2}{\beta _3} - {n_3}{\beta _2}} \right)} & 0 \cr } } \right)$$

A strain tensor must be symmetrical. A rotation tensor must be antisymmetric. The rotation tensor must also have no normal components. The strain tensor εij is the one used in calculations.

Volumetric strain

The sum of the diagonal elements of the strain tensor is the volumetric strain or dilatation:

$${{\Delta V} \over V} = {\varepsilon _{11}} + {\varepsilon _{22}} + {\varepsilon _{33}} = \Delta $$