DoITPoMS

back

Hexagonal close-packed crystals: the axial ratio

The ideal axial ratio (c/a) for a hexagonal close-packed crystal structure can be calculated by considering non-interacting hard spheres packed in an h.c.p. lattice.

If the sphere radius is r, then the lattice parameters a (= b) and c can be written in terms of r:

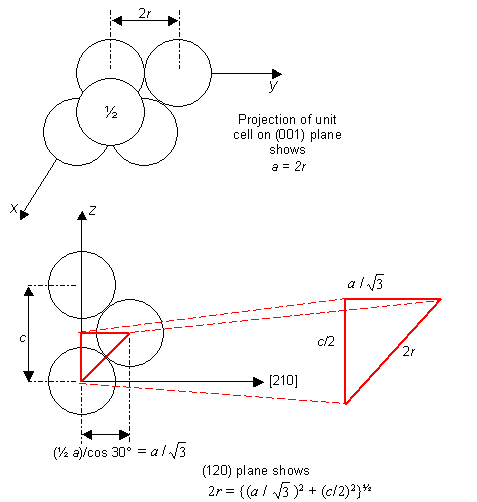
These two relationships can be solved for the ideal axial ratio c/a:

a² = a²/3 + c²/4

4 = 4/3 + c²/a²

c/a = 1.633

Many materials have the hexagonal P crystal system, but the axial ratio is rarely ideal. Cadmium, for example, has an axial ratio of c/a = 1.886. This non-ideal structure has implications for the behaviour of the material, for example in slip.

back