Dissemination of IT for the Promotion of Materials Science (DoITPoMS)

DoITPoMS Teaching & Learning Packages Slip in Single Crystals Slip in HCP metals 2: application of Schmid's Law
Slip in Single Crystals AimsBefore you startIntroductionSlip geometry: the critical resolved shear stressGeometry during slipSlip in HCP metals 1: slip systemsSlip in HCP metals 2: application of Schmid's LawSlip in HCP metals 3: calculation of forcesSlip in HCP metals 4: observing slip in cadmiumVideo clips of slip in a single cadmium crystalExercise: Determination of the critical resolved shear stress for slip in cadmiumSlip in CCP metalsSummaryQuestionsGoing further
TLP creditsTLP contentsShow all content
Viewing and downloading resourcesAbout the TLPsTerms of useFeedbackCredits Print this page
PreviousNext

Slip in HCP metals 2: application of Schmid's Law

The analysis of slip in h.c.p. crystals can be demonstrated by considering the special case in which the slip direction, the tensile axis and the normal of the slip plane are all coplanar. In this special case, φ + λ = 90°. This condition is not generally true.

For example, consider a cadmium single crystal strained with the tensile axis along the [021] direction. Cadmium is (approximately) hexagonal close-packed with a = b = 2.98 Å and c = 5.62 Å, and it slips on <100>{001}. The slip plane must be (001), since that is the only plane of the {001} type. Hence, the slip plane normal is parallel to [001]. The tensile axis [021] and the slip plane normal [001] both lie in the (100) plane.

The operating slip system will be that with the highest resolved shear stress acting upon it. By considering the geometry, shown in the diagram below, it is apparent that the primary slip system (i.e. the system with the greatest Schmid factor) in h.c.p. crystals will be [010](001) for all tensile axes of the [0VW] type.

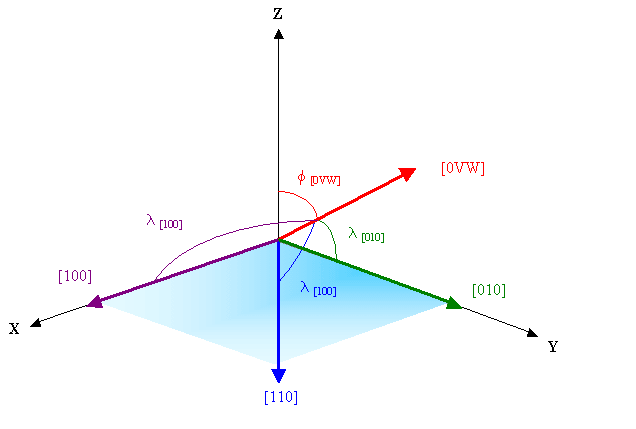
Diagram illustrating slip geometry

Geometry of slip in a hexagonal close-packed crystal system. The angle between the [100] and [010] directions is 120°. The three possible slip systems are [100](001), [010](001) and [110](001). For a tensile axis lying in the (100) plane of the type [0VW], the angle between the slip direction and the tensile axis is smallest for the [010] slip direction. cos φ cos λ is largest when λ = λ[010], hence the operating slip system is [010](001).

PreviousNext