Which slip system will operate?
Calculating the Schmid factor for each slip system is possible but can be complicated and time-consuming, depending on the crystal structure and the orientation of the tensile axis. For some cubic structures, there are two short cuts for finding the slip system that will operate. These methods work only for cubic crystals that slip on <1 bar1 0> {111} or <1 bar1 1> {110}, i.e. cubic close-packed (c.c.p) or body-centred cubic (b.c.c.) metals respectively.
The OILS rule: example for a c.c.p. metal
- Write down the indices of the tensile axis [UVW]
- Ignoring the signs, identify the highest (H), intermediate (I) and lowest (L) valued indices.
- The slip direction is the <110> direction with zero in the position of the Intermediate index and the signs of the other two indices preserved.
- The slip plane is the {111} plane with the signs of the Highest and Intermediate indices preserved, but with the sign of the Lowest index reversed.
OILS stands for zerO Intermediate, Lowest Sign. The method works equally well for bcc metals in which the directions are of the form <111> and the planes {110}.
Example: In a c.c.p metal, if the tensile axis is along [214] the indices are identified as [ILH].
So zerO Intermediate gives the slip direction as [011], and Lowest Sign tells us that the slip plane is (1 bar1 1). Hence the slip system with the greatest Schmid factor is [011](1 bar1 1).
Diehl's Rule
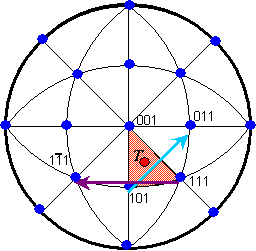
This method also works for c.c.p. and b.c.c. crystals, but requires some knowledge of stereograms. It can be shown that Diehl's rule is exactly equivalent to the OILS rule, so if you have not studied stereograms, there is no need to learn Diehl's method.
Diehl's Rule: example for a c.c.p. metal
- Draw a cubic stereogram displaying all poles of the forms {100}, {110} and {111}, and the great circles which connect them, as shown above. NB: In the above sketch, only relevant poles have been labelled, to preserve clarity.
- Your diagram will show 48 standard triangles. Locate the triangle that contains the pole of the tensile axis (TA). For example, in the above diagram the TA lies in the 001-101-111 spherical triangle, which has been shaded.
- The slip plane in a c.c.p. crystal must be of the form {111}. To identify the operational slip plane, take the {111}-type pole in the shaded triangle and form its reflection in the side opposite to it, i.e. follow the purple arrow above. In this case the slip plane is (1 bar1 1).
- Similarly, the slip direction must be of the <110> type. Take the reflection of the <110>-type pole in the side opposite to it to find the actual slip direction, i.e. the blue arrow. Hence for this example, the slip direction is [011].
For a b.c.c. metal, the same method can be used by interchanging the slip plane and slip direction indices, so that directions are of the form <111> and planes are of the form {110}. If the tensile axis lies at the boundary of two or more triangles, then the Schmid factors of each corresponding slip systems are equal.

