Anisotropic diffusion
The rate of diffusion of a specific atomic species is measured in terms of the coefficient of diffusion, D, which relates the flux of atoms (number crossing unit area in unit time) to the concentration gradient. In an isotropic material:
J = -D(gradc)
where J = flux (number per unit area per unit time) of an atomic species across a plane normal to the concentration gradient, gradc. The negative sign indicates that the flux is from high to low concentrations. For an isotropic material, such as an amorphous solid, the diffusion coefficient is independent of temperature.
Flux and concentration gradient are both vectors, so the coefficient of diffusion is a second rank tensor in an anisotropic material. The diffusion is anisotropic and can be described by three principal values of D, in the same way as thermal and electrical conductivity. (Note: we are not concerned here with the dependence of diffusion on temperature).
Example: Diffusion of Ni in Olivine, (Mg,Fe)2SiO4
Olivine is the name for a series of minerals between two end members, fayalite (Fe2SiO4) and forsterite (Mg2SiO4). The two minerals form a solid solution where the iron and magnesium atoms can be substituted for each other without significantly changing the crystal structure. Olivine has an orthorhombic structure. The lattice parameters depend on the precise composition, but a typical set of values is: a = 0.49 nm, b = 1.04 nm, c = 0.61 nm.
The principal values of D for diffusion of nickel atoms in olivine also depend on the precise composition of the olivine. One set of values for an unspecified composition at 1423 K (1150ºC) is:
Dx = 4.40 x 10-18 m2s-1
Dy = 3.35 x 10-18 m2s-1
Dz = 124.0 x 10-18 m2s-1
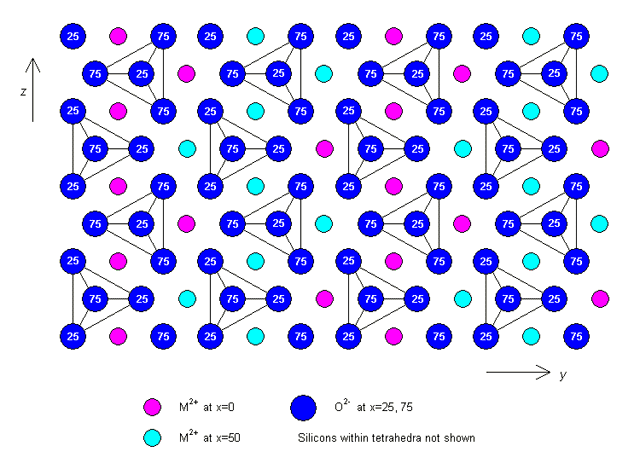
where the values correspond to the diffusion coefficients along the x, y and z crystallographic axes respectively. The exact values are unimportant for this discussion, but it is important to appreciate that diffusion occurs much faster parallel to the z-axis than in directions in the plane perpendicular to it. This happens because of the way in which the atoms are arranged in the crystal structure, a plan view of which is shown below (projected down the x-axis).
Note that x = 0, 25, 50 and 75 represent the x-coordinates of the atoms (as a percentage of the unit cell dimension a).
Crystal structure of olivine (click on image to view a larger version)
As you can see, there are chains of M2+ sites (where M2+ represents a metal ion, in this case either Mg or Fe) parallel to the z-axis. Diffusion occurs by Ni2+ substituting for M2+ along these chains, making diffusion in this direction much faster than in any other.
Rotatable model of the olivine structure
Fast ion conduction
When the structure of a solid material contains a large number of vacant sites (as a consequence of its composition), then it is likely to show high ionic mobility for some species of ion (sometimes an anion, sometimes a cation), even at modest temperatures. A high ionic mobility means that charge can be transferred very easily, and conductivities can approach those of aqueous electrolyte solutions or molten salts.
For a material to be a fast ion conductor, there should be:
- a high concentration of charge carriers
- a high concentration of vacant sites in the structure
- a low activation energy for ionic migration
There are a number of different types of fast ion conductors. The material may be either a cationic or an anionic conductor, depending on the charge of the mobile ion. The material may also have a fully ionic structure, or the mobile ions may be in a covalent host structure. The dimensionality of the mobility can also vary: the ions may move through channels (1D), within layers of a structure (2D), or throughout the whole structure (3D).
Examples of fast ion conductors
1D fast ion conductors: Tungsten Bronzes, MxWO3
In these materials, WO3 tetrahedra or octahedra form a covalent network. Usually either M+ or M2+ (for example Na+ or Cu2+) are the mobile ions, and these move along channels in the structure. As a result, the conductivity is very high in this direction. An example of a tungsten bronze is shown below, projected along the z-axis, which is parallel to the channel direction.
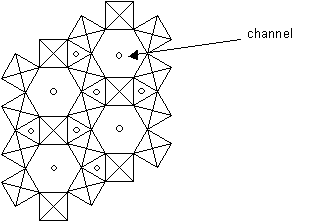
Structure of tungsten bronze
2D fast ion conductor: Sodium beta-alumina, Na β-Al2O3
Sodium beta-alumina consists of blocks of γ-alumina (which has a spinel structure, the details of which need not be considered here) connected by a layer of bridging oxygen and sodium ions. Not all the Na+ sites are occupied, and conduction occurs by the movement of the ions within this layer.
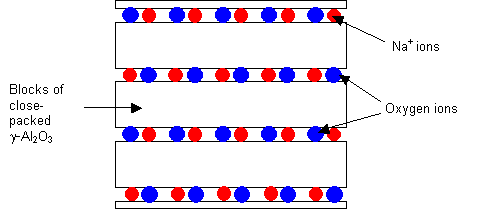
Structure of sodium beta-alumina