Anisotropic thermal conductivity
When a temperature gradient is present in a material, heat will always flow from the hotter to the colder region to achieve thermal equilibrium. As mentioned in the introduction, thermal conductivity is the property that relates heat flow to the temperature gradient. In an isotropic material:
\[J = k{{dT} \over {dr}}\]
where J = heat flow, k = thermal conductivity, and dT/dr = temperature gradient.
Anisotropic thermal conductivity in quartz.
In quartz, perpendicular to the c-axis, the thermal conductivity is 6.5 Wm-1K-1. However, the thermal conductivity parallel to c is 11.3 Wm-1K-1.
The anisotropic thermal conductivity of quartz can easily be seen using a simple demonstration. Two sections cut from a quartz crystal, one perpendicular to the c-axis, and one parallel to it, are in turn mounted as shown in the diagram below. Pieces of plastic containing a heat sensitive liquid crystal are then glued to the top surfaces and the sections are heated from a point at their centre, using a soldering iron. As the quartz heats up, the heat sensitive film changes colour, which allows us to see how quickly the heat is conducted away from the centre. The colours indicate contours of constant temperature.
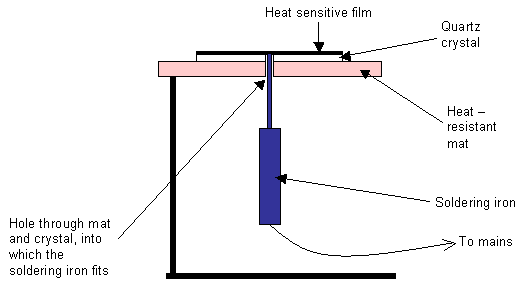
Diagram of experimental apparatus
When heating the section cut perpendicularly to the c-axis, the observed shape is a circle, showing that the thermal conductivity is the same in all directions in this plane. However, when using the section cut parallel to the c-axis, the shape seen is an ellipse, which shows that the thermal conductivity in this plane is direction-dependent.
Video of a section of quartz cut perpendicular to the c axis being heated from a point at its centre
Video of a section of quartz cut parallel to the c axis being heated from a point at its centre
Flow Properties
The heat flow does not have to be parallel to the thermal gradient. A result of this can be seen by considering one-dimensional conduction in a long rod and a thin plate, both made of the same anisotropic material, arranged so that the normal to the plate and the length of the rod are oriented in an arbitrary general direction.
Thin Plate
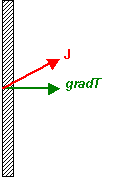
Here the geometry of the set-up constrains the temperature gradient to be perpendicular
to the plate. Due to the anisotropic nature of the material, the heat flux, J,
will be in the direction shown, say. However, the thermal conductivity
perpendicular to the plate is defined as the component of the heat flux parallel
to the temperature gradient, j||, divided by the magnitude
of that gradient. Thus:
\[{k_{||}} = {{{j_{||}}} \over {gradT}}\]
Rod
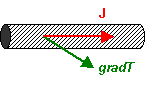
Now the heat must flow along the rod, and the temperature gradient will be in a different
direction, as shown. Here the thermal resistivity is defined as the component
of the temperature gradient parallel to the rod, gradT||,
divided by the magnitude of the heat flux. Thus:
\[{\rho _{||}} = {{grad{T_{||}}} \over J}\]
where ρ is the resistivity.
These definitions hold for any situation where the heat flux and the thermal gradient are not parallel in an anisotropic material, in isotropic materials they will be parallel. It is important to realise that in anisotropic materials
\[{\rho _{||}} \ne {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {{k_{||}}}}}\right.\kern 0.01em} \!\lower0.7ex\hbox{${{k_{||}}}$}}\]
except along the principal axes. Only in isotropic materials is the resistivity always the reciprocal of the conductivity, and vice versa.
Note: By using a large, thin plate and a long rod, the effects of the alterations in the directions of heat flow and temperature gradient close to the edges (of the plate) or ends (of the rod) - "edge effects" and "end effects" - affect only a very small proportion of the sample and can be ignored.
More broadly, anisotropic properties should be represented as tensors, for example thermal conductivity can be written:
\[{j_i} = {k_{ij}}{(gradT_j)}\]
and the thermal resistivity can be written:
\[{gradT_i} = {\rho_{ij}}{j_j}\]
where kij and ρij are second rank tensors, see Tensors in Materials Science.

