Radius-normal property of the representation ellipsoid

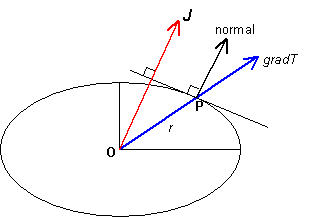
As previously described, the heat flux, J, in an anisotropic material is related to the temperature gradient, gradT, by:

J = k(gradT)

The components of the temperature gradient parallel to the principal axes (x, y and z) will be:

\[grad{T_x} = (gradT)l grad{T_y} = (gradT)m grad{T_z} = (gradT)n\]

where l, m and n are the direction cosines specifying the direction of gradT, and for example, l is the cosine of the angle between the x-axis and the thermal gradient vector.

Therefore, the components of the heat flow are:

\[{j_x} = {k_1}(gradT)l\;\;\; {j_y} = {k_2}(gradT)m \;\;\; {j_z} = {k_3}(gradT)n\]

where k₁, k₂ and k₃ are the values of thermal conductivity along the principal axes, x, y and z, and are called the principal values.

The direction cosines of J> are therefore proportional to k₁l, k₂n, n₃n.

We have already shown that the equation for the representation ellipsoid is

\[{k_1}.{x^2} + {k_2}.{y^2} + {k_3}.{z^2} = 1\]

Suppose P is a point on the surface of the ellipsoid such that OP is parallel to the temperature gradient. The coordinates of P are therefore rl, rm, rn), where r is the distance OP.

\[r^2 = {k_1}{x^2} + {k_2}{y^2} + {k_3}{z^2}\]

The components of the gradient at (x₁ y₁z₁) are obtained by partial differentiation of this equation, which gives components in the directions of the x, y, and z axes of:

\[2r{{{\rm{d}}r} \over {{\rm{d}}x}} = 2{k_1}{x_1}\;\;\;2r{{{\rm{d}}r} \over {{\rm{d}}x}} = 2{k_2}{y_1}\;\;\;2r{{{\rm{d}}r} \over {{\rm{d}}x}} = 2{k_3}{z_1}\]

The components are therefore equal to

\[\left( {{{{k_1}{x_1}} \over r} , {{{k_2}{y_1}} \over r} , {{{k_3}{z_1}} \over r}} \right)\]

But since

x₁ = rl, y₁ = rm, z₁ = rn

the normal at P has direction cosines proportional to k₁l, k₂m, k₃n. Hence the normal at P is parallel to the heat flux.