Tensors

Tensor analysis can be used to describe this situation. Consider an anisotropic material with principal axes 1, 2 and 3. For sake of example, a temperature gradient, gradT, is applied in an arbitrary direction perpendicular to the 3-axis, non-parallel to the principal axes 1 and 2. The resulting heat flow, J, will not be parallel to the temperature gradient. The components of these vectors parallel to the principal axes are as shown in the diagram below.

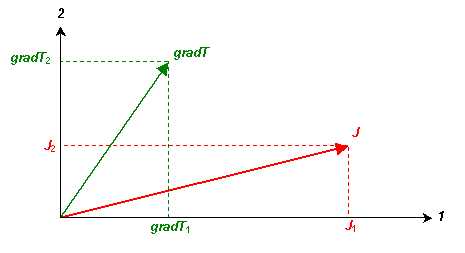
As mentioned before, J = k(gradT). Using tensor notation to describe the above situation,

J₁ = k₁₁(gradT₁), J₂ = k₂₂(gradT₂), and J₃ = 0

In general,

J_i = k_ij(gradT_j)

where the suffices i and j represent the relevant axes. This equation summarises the following matrix equation:

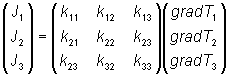
Here J_i and gradT_j are first rank tensors (one suffix) and k_ij is second rank (two suffices). Since 1, 2 and 3 are the principal axes then the k_ij tensor is a diagonal matrix - all values are zero unless i = j. If an arbitrary set of axes is chosen, then it will be a general matrix.

Other second rank tensors, which relate first rank tensors, include:

• Electrical conductivity, relating current density to electric field
• Permittivity, relating dielectric displacement to electric field
• Permeability, relating magnetic induction to magnetic field

Thermal expansion is also a second rank tensor, but it relates strain (a second rank tensor) to temperature change (a scalar - zero rank).