Lattice geometry
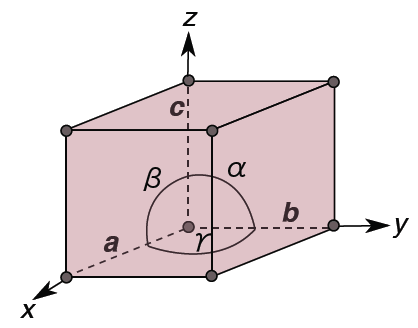
To define the geometry of the unit cell in 3 dimensions we choose a right-handed set of crystallographic axes, x, y, and z, which point along the edges of the unit cell. The origin of our coordinate system is at one of the lattice points.
Lattice parameters
The length of the unit cell along the x, y, and z direction are defined as a, b, and c. Alternatively, we can think of the sides of the unit cell in terms of vectors a, b, and c. The angles between the crystallographic axes are defined by:
α = the angle between b and c
β = the angle between a and c
γ = the angle between a and b
a, b, c, α, β, γ are collectively known as the lattice parameters (often also called ‘unit cell parameters’, or just ‘cell parameters’).
Lattice vectors
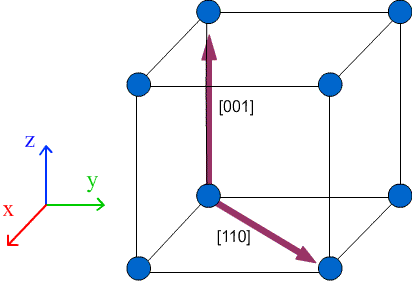
A lattice vector is a vector joining any two lattice points. Any lattice vector can be written as a linear combination of the unit cell vectors a, b, and c:
t = U a + V b + W c
In shorthand, lattice vectors are written in the form:
t = [UVW]
Negative values are not prefixed with a minus sign. Instead a bar is placed above the number to denote that the value is negative:
t = −U a + V b − W c
This lattice vector would be written in the form:
t = [V]
Lattice directions are written the same way as lattice vectors, in the form [UVW]. The direction in which the lattice vector is pointing is the lattice direction. The difference between lattice directions and lattice vectors is that a lattice vector has a magnitude which can be shown by prefixing the lattice vector with a constant. By convention U, V and W are integers.
Many crystal systems have elements of symmetry. In these systems, certain sets of directions are symmetrically equivalent to each other. The set of directions that are symmetrically related to the direction [UVW] are written <UVW>.

