Dissemination of IT for the Promotion of Materials Science (DoITPoMS)

DoITPoMS Teaching & Learning Packages Crystallography Symmetry
Crystallography AimsBefore you startIntroductionLatticesUnit CellLattice geometryCrystal structureClose packing and packing efficiencySymmetryCombining symmetryCrystal systemsSummaryQuestionsGoing further
TLP creditsTLP contentsShow all content
Viewing and downloading resourcesAbout the TLPsTerms of useFeedbackCredits Print this page
PreviousNext

Symmetry

We have already met the concept symmetry in relation to crystal structures: the lattice generates the translational symmetry—the motif is repeated on every lattice point.

Other types of symmetry exist, including:

  • rotation axes
  • mirror planes
  • centre of symmetry
  • inversion axes (combination of rotation and centre of symmetry operations)

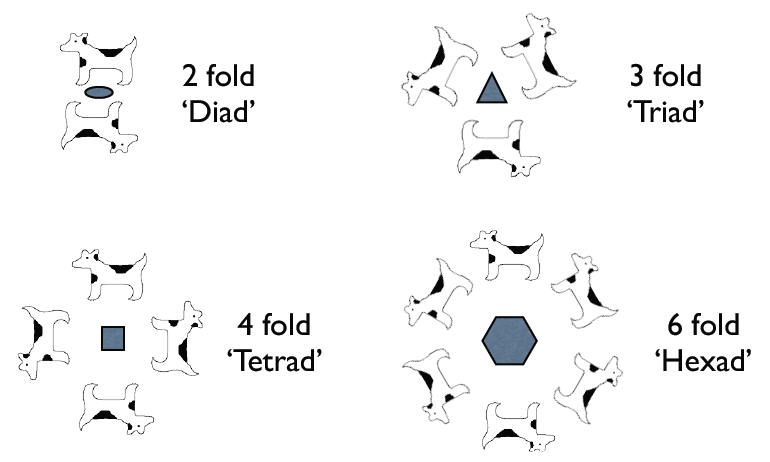
An n fold rotational symmetry operation rotates an object by 360°/n. Only n = 1, 2, 3, 4, and 6 are permitted in a periodic lattice

Examples of n-fold rotational symmetry

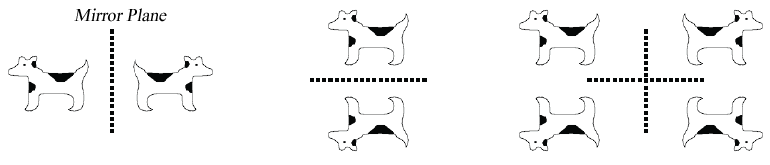
An object has mirror symmetry if reflection of the object in a plane brings it into coincidence with itself:

Examples of mirror symmetry

Some objects have special symmetry about an origin such that, for any point at position x, y, z, there is an exactly similar point at –x, –y, –z. The origin is called a centre of symmetry ( “inversion centre”). Such an object is said to be centrosymmetric:

An n-fold inversion axis is a combination of a rotation by 360/n followed by a centre of symmetry operation. An example of a 4-fold inversion axis is show in the following animation:

PreviousNext