Dissemination of IT for the Promotion of Materials Science (DoITPoMS)

DoITPoMS Teaching & Learning Packages Diffusion Derivation of Fick's second law
Diffusion AimsBefore you startIntroductionDiffusion mechanismsRandom walkFick's first lawFick's second lawInterdiffusionMicrostructural effectsTemperature EffectsApplications of DiffusionSummaryQuestionsGoing further
TLP creditsTLP contentsShow all content
Viewing and downloading resourcesAbout the TLPsTerms of useFeedbackCredits Print this page
PreviousNext

Derivation of Fick's second law

Consider a cylinder of unit cross sectional area. We take two cross-sections, separated by δx, and note that the flux through the 1st section will not be the same as the flux through the second section.

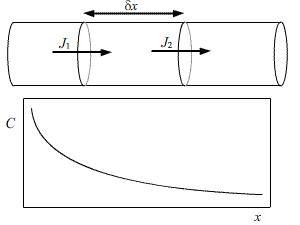
Diagram of flux through 2 sections of cylinder

From Fick’s first law we can deduce that:

\[{J_1} = - D{\left\{ {\frac{{\partial C}}{{\partial x}}} \right\}_1}\] \[{J_2} = - D{\left\{ {\frac{{\partial C}}{{\partial x}}} \right\}_2}\] \[{J_2} = - D{\left\{ {\frac{{\partial C}}{{\partial x}}} \right\}_1} + \partial x\left\{ {\frac{{{\partial ^2}C}}{{\partial {x^2}}}} \right\}\]

In an increment of time,δt, there is a corresponding increment in concentration, δC.

\[\partial C\partial x = ({J_1} - {J_2})\partial t\] \[\frac{{\partial C}}{{\partial t}} = D\left\{ {\frac{{{\partial ^2}C}}{{\partial {x^2}}}} \right\}\]

This is Fick’s second law

PreviousNext