If a material contains grains, the grains will act as diffusion pathways, along which diffusion is faster than in the bulk material.
Note: This animation requires Adobe Flash Player 8 and later, which can be downloaded here.
Consider a cylindrical grain of radius r and grain boundary thickness δ
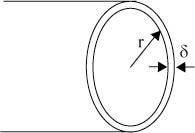
The area of the grain boundary in the cross section is 2π r δ.
Every grain boundary is shared between two grains, so the total grain boundary area associated with one grain is π r δ.
The ratio of the area of the grain boundary to the bulk is:
The overall flux through unit cross-sectional area is the sum the fluxes through the bulk and the grain boundary:
The derivation for this equation is here
Therefore:
It is important to realise that δ is very small, therefore grain boundary diffusion only becomes significant when Dgb >> Db, i.e. at low temperatures.
The following animation shows the effect of microstructure on diffusion at various temperatures:
Note: This animation requires Adobe Flash Player 8 and later, which can be downloaded here.
Dislocations have a similar effect, providing fast diffusion paths due to the disruption in the lattice, again with only a significant effect at low temperatures.
previous | next
© 2004-2013 University of Cambridge.