The Gibbs phase rule
The Gibbs phase rule links the number of phases, number of components and number of degrees of freedom in a system.
A phase (p) can be defined as the homogenous regions of a system. Phases are separated from each other by bounding surfaces. A system which contains one phase when in equilibrium is known as homogenous. If a system has more than one phase present in equilibrium, then it is known as heterogenous. In heterogeneous systems, it is (at least in theory) possible to mechanically separate the various phases from each other.
The number of components in a system (c) is analogous to a set of basis vectors for a space. It is the smallest number of independent variables required to completely describe the composition of all of the phases in the system. In a unary system (where a material of a single composition is considered) the number of components is one. In a binary system (like where two metals are mixed together to form an alloy) the number of components is two and the composition is represented as a line going from 100% of one component to 100% of the other component.
The number of degrees of freedom of an equilibrium state (f) is the number of variables (composition variable, temperature or pressure) that must be specified to define the state of a system.
Derivation of the Phase Rule
The composition of each phase in a system is defined by c−1 variables. By specifying the proportion of c−1 components, the proportion of the last one is defined (as the fraction of each proportion must sum to 1). In a binary system, stating that there is X% of one component implies that there is (1−X)% of the other component.
There are p phases in a system. It follows that the number of compositional variables in the system is then p(c−1) - the number of phases multiplied by the number of variables per phase.
The total number of variables in the system is given by p(c−1)+2 – the number of compositional variables plus a variable each for pressure and temperature.
The number of degrees of freedom in the system is given by the difference of the total number of variables in the system and the number of variables that are set by specifying that the system is in equilibrium.
A requirement for a system to be in equilibrium is that the chemical potential of each component is the same in each phase.
There are p−1 independent equations describing each component in each phase. By specifying the chemical potential are equal to each other in all combinations of phases but one, the fact that they are equal in this final pair of phases is implied. It is a dependent equation (can be constructed from the others) so is not considered.
When the system is defined to be in equilibrium, c(p−1) variables are specified (p−1 for each component, multiplied by the number of components).
The number of degrees of freedom is therefore:
Degrees of freedom = total variables − specified variables
\[ f = p(c-1)+2-c(p-1) \]Simplifying:
\[ f + p = c + 2 \]This is known as the Gibbs phase rule.
Applying the Gibbs Phase Rule
Unary Systems
In a unary system, the number of components is one, c = 1.
The total number of degrees of freedom and phases possible is therefore three.
There can be:
- One phase and two degrees of freedom
- Two phases and one degree of freedom
- Three phases and no degrees of freedom
There cannot be a case where no phases exist.
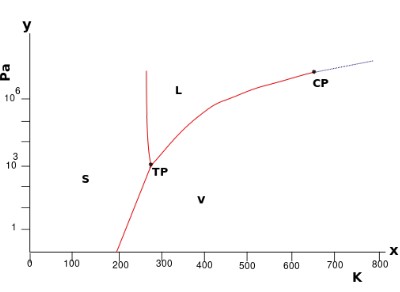
Consider the pressure-temperature phase diagram for water:
By Eurico Zimbres - Own work, CC BY-SA 2.5, https://commons.wikimedia.org/w/index.php?curid=1173910
It is a unary phase diagram. There is one component – water.
In the single-phase regions (solid, liquid and vapour) there are two degrees of freedom. The equilibrium is bivariant. The system can lie on any point in this region so both the temperature and pressure must be specified to define the state of the system.
Both the temperature and the pressure can be altered without moving out of the single-phase region.
Two phase equilibria are represented by the lines bounding the single-phase regions. These lines are pressure – temperature conditions where two phases can coexist. On these lines, there is one degree of freedom. The equilibrium is univariant.
By specifying the temperature or pressure, the other variable is constrained (as the system must lie on the bivariant line). Only one variable is needed to define the system.
Three phase equilibria (which exists at the triple point here) have no degrees of freedom. They are invariant equilibria. The invariant point has a set temperature and pressure so requires no variables to be specified.
By stating that the system is in an invariant equilibrium, the temperature and pressure are implied.
Binary Systems
In a binary system the number of components is two, c = 2. The total number of degrees of freedom and phases is four.
As binary systems are often considered on composition-temperature phase diagrams, pressure is fixed. This removes a degree of freedom (as changing the pressure requires moving off the plane of the binary phase diagram).
For a constant pressure (or equally a constant temperature), the total number of phases and degrees of freedom is three.
There can be:
- One phase and two degrees of freedom
- Two phases and one degree of freedom
- Three phases and no degrees of freedom<
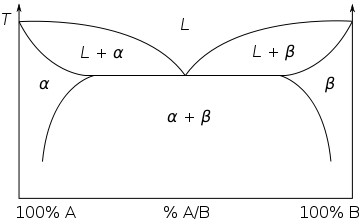
Consider a simple binary eutectic phase diagram:
By Eutektikum.gif: Dr. Báder Imrederivative work: Michbich (talk) - Eutektikum.gif, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=8394880
Single phase regions are areas where the alloy can lie on any point in the region.
Single phase regions have two degrees of freedom. These are bivariant equilibria. Both a temperature and a composition must be specified to define the state of the system.
Two phase regions can be thought of as a stack of isothermal tie lines. Each end of the tie line gives the composition of the phases at that temperature. The bounding curves of the two-phase regions are mapped out by the ends of these tie lines.
Two phase regions are areas, and the alloy can lie on any tie line within the area.
Two phase regions only have one degree of freedom, they are univariant equilibria.
By specifying the temperature, the relevant tie line can be identified and the compositions of the two phases determined, defining the state of the system.
Similarly, by specifying the composition of one of the two phases, the relevant tie line can be identified and from it the temperature and the composition of the other phase determined. By specifying that there are two phases in equilibrium and one variable, the system is defined.
Three phase regions have no degrees of freedom. They are invariant equilibria. They are points on the phase diagram with a fixed temperature and composition. The invariant point in this phase diagram is the eutectic point where alpha, beta and the liquid are the three phases in equilibrium. The temperature and composition cannot be changed without moving off of the invariant point.
Reactions are often associated with invariant points as heating or cooling through an invariant point can cause a dramatic change in the phases present. Some examples of invariant reactions in binary systems are:
Eutectic \( \rm{L \rightleftharpoons \alpha + \beta} \) seen in Ag-Cu, Al-Si, Sn-Bi and Fe-C systems
Peritectic \( \rm{L + \alpha \rightleftharpoons \beta} \) seen in Cu-Zn, Cu-Sn and Fe-C systems
Eutectoid \( \rm{\alpha \rightleftharpoons \beta + \gamma} \) seen in Fe-C system
Peritectoid \( \rm{\alpha + \beta \rightleftharpoons \gamma} \) seen in Al-Cu system
Monotectic \( \rm{L_1 \rightleftharpoons L_2 + \alpha} \) seen in Cu-Pb system
Metatectic \( \rm{\alpha \rightleftharpoons \beta + L} \) seen in Ag-Li system
Syntactic \( \rm{L_1 + L_2 \rightleftharpoons \alpha} \) seen in K-Zn system
Limitations of the Gibbs Phase Rule
The Gibbs phase rule determines what combination of phases and degrees of freedom are possible in a system. It cannot inform on which kinds of equilibria are present in each system, simply the nature of those equilibria if they were present.

