Behaviour of the Fermi Energy
The Fermi-Dirac distribution was introduced in the section The Fermi-Dirac Distribution. The relevant equation to describe the distribution is
\[f\left( E \right) = \frac{1}{{\exp \left( {\left( {E - E_{\rm{F}} } \right)/{k_{\rm{B}}}T} \right) + 1}}\]
so that for a Fermi energy, \( E_{\rm{F}} \), of 5 eV, the distribution takes the form
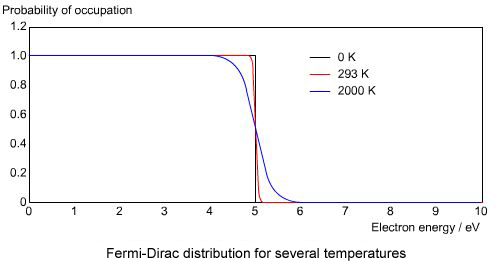
as a function of temperature.
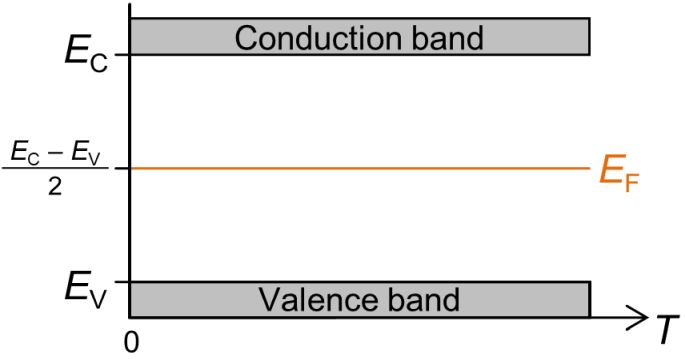
One feature that is very important about the Fermi-Dirac distribution is that it is symmetric about the Fermi energy. Hence for a simple intrinsic semiconductor, which has equal numbers of electrons in the conduction band and holes in the valence band, the Fermi energy must lie halfway between the valence band and the conductance band, regardless of the temperature, because each electron promoted to the conduction band leaves a hole in the valence band. This is shown in the band diagram below in which energy is plotted vertically against temperature horizontally.
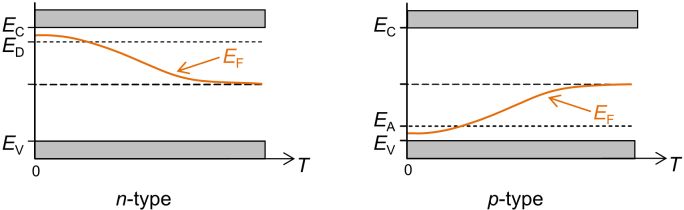
For an extrinsic semiconductor the situation is slightly more complicated. At absolute zero in an n-type semiconductor, the Fermi energy must lie in the centre of the gap between the donor level and the bottom of the conduction band. At low temperatures in such a semiconductor there are more conduction electrons than there are holes. If the donor level is more than half full, the Fermi energy must lie somewhere between the donor levels and the conduction band. At higher temperatures, when the donor level is completely depleted of electrons, and the contribution from intrinsic electrons to the overall electrical conductivity becomes more substantial, the Fermi energy tends towards that for an intrinsic semiconductor, i.e., halfway between the conduction and valence bands, and therefore in the middle of the band gap.
For p-type semiconductors the behaviour is similar, but the other way around, i.e., the Fermi energy starts midway between the valence band and the acceptor levels at absolute zero. It gradually increases as the temperature increases, so that at high temperatures it lies in the middle of the band gap as well.