Dissemination of IT for the Promotion of Materials Science (DoITPoMS)

DoITPoMS Teaching & Learning Packages Thermal Expansion and the Bi-material Strip Results: Measurement of Young's modulus
Thermal Expansion and the Bi-material Strip AimsBefore you startIntroductionExperiment: Measurement of Young's modulusResults: Measurement of Young's modulusSimulation: Measurement of Young's modulusOrigin of thermal expansionThe bi-material stripExperiment: Estimating the boiling temperature of nitrogenResults: Estimating the boiling temperature of nitrogenExperiment: Measuring the thermal expansivity of polycarbonateResults: Measuring the thermal expansivity of polycarbonateSummaryQuestionsGoing further
TLP creditsTLP contentsShow all content
Viewing and downloading resourcesAbout the TLPsTerms of useFeedbackCredits Print this page
PreviousNext

Results: Measurement of Young's modulus

A set of results for the steel strip are given below.

load, m (kg)
deflection, δ (10-3 m)
0 0
0.05 3
0.10 6.5
0.15
9
0.20 13
0.25
16

 

A graph of these results gives:

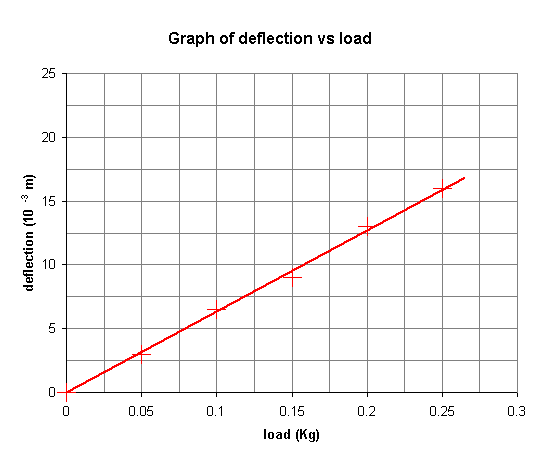
Graph of deflection vs load

The gradient of this graph is

\[{\rm{gradient}} = \frac{{16 \times {{10}^{ - 3}}}}{{0.25}} = 6.4 \times {10^{ - 2}}{\rm{mk}}{{\rm{g}}^{ - 1}}\]

In addition

width of strip (w) = 0.01 m
thickness of strip (h) = 0.001 m
length of strip (L) = 0.15 m

So, using equation (2)

\[{\rm{gradient}} = \frac{{0.01 \times {{0.001}^3}}}{{12}} = 8.3 \times {10^{ - 13}}{{\rm{m}}^3}\]

From equation (1) with P = mg, a graph of δ against m will have a gradient

\[{\rm{gradient}} = \frac{1}{3}\frac{{g{L^3}}}{{EI}}\]

and hence

\[E = \frac{1}{3}\frac{{g{L^3}}}{{{\rm{gradient}} \times I}} = \frac{{9.8 \times {{0.15}^3}}}{{3 \times 6.4 \times {{10}^{ - 2}} \times 8.3 \times {{10}^{ - 13}}}} = 2.1 \times {10^{11}}{\rm{Pa(2s}}{\rm{.f}}{\rm{.)}}\]

So the steel from which the strip is made has a Young's modulus of 210 GPa (close to the figure given in the properties table).

Repeating the experiment for the aluminium and polycarbonate strips gives Young's moduli of 70 GPa and 5.5 GPa respectively. These results will be used later in the TLP.

PreviousNext