Extrusion: assuming sliding on die face
The mathematics behind the equation for pmin:
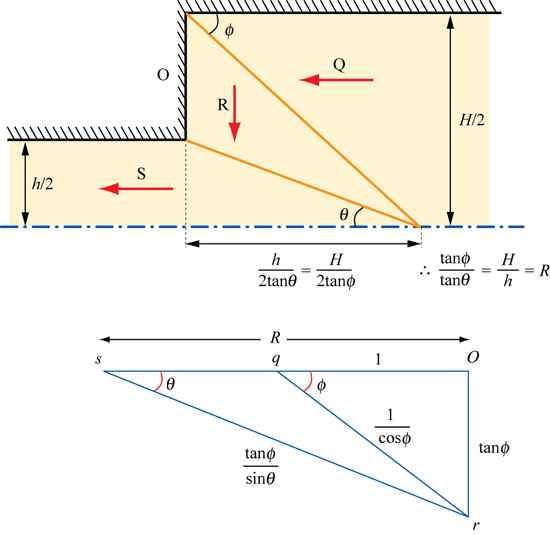
To analyse this situation, it is convenient to define angle Osr
in the hodograph as θ and angle Oqr
as φ . Thus the plane of shear between R
and S makes an angle θ with the horizontal
extrusion axis and the plane of shear between Q
and R makes an angle φ with the horizontal
extrusion axis.
Let Oq be a velocity vector of unit magnitude in the hodograph, i.e. νOq = 1
Hence,
\[{\nu _{Or}} = \tan \phi ,\;\;{\nu _{qr}} = \frac{1}{{\cos \phi }},\;\;{\nu _{rs}} = \frac{{\tan \phi }}{{\sin \theta }}\;\;and\;\; {\nu _{Os}} = R\]
where R is the extrusion ratio = H/h
From the diagram of the extrusion process it follows that
\[\frac{h}{{2\tan \theta }} = \frac{H}{{2\tan \phi }}{\rm{ \;\; and\;\; so \;\; }}R = \frac{H}{h} = \frac{{\tan \phi }}{{\tan \theta }}\]
Applying the general formula
$$pa = k\sum\limits_n {\left| {{\rm{SS}}{'_n}} \right|} \left| {{v_{sn}}} \right|$$
we then have
\[p\frac{H}{2} = k\left\{ {{\rm{QR}}{v_{qr}} + {\rm{RS}}{v_{rs}}} \right\}\]
where QR is the length of the line dividing regions Q and R and RS is the length of line dividing regions R and S in the diagram of the extrusion operation.
Now,
$${\rm{QR}} = \frac{H}{{2\sin \varphi }}{\rm{ \;\; and \;\; RS}} = \frac{H}{{2\sin \theta }}$$
and so
$$R = \frac{{{A_0}}}{{{A_1}}} = \frac{H}{h}$$
$$p\frac{H}{2} = k\left\{ {\frac{H}{{{\rm{2sin}}\phi }}.\frac{1}{{\cos \phi }} + \frac{h}{{{\rm{2sin}}\theta }}.\frac{{\tan \phi }}{{\sin \theta }}} \right\}$$
$$ = k\left\{ {\frac{H}{{{\rm{2sin}}\phi }}.\frac{1}{{\cos \phi }} + \frac{H}{{{\rm{2sin}}\theta }}.\frac{{\tan \theta }}{{\sin \theta }}} \right\}$$
substituting for h tanφ. Hence,
$$p = k\left\{ {\frac{1}{{{\rm{sin}}\varphi \cos \varphi }} + \frac{1}{{\sin \theta \cos \theta }}} \right\}$$
Now,
$$\frac{1}{{{\rm{sin}}\varphi \cos \varphi }} = \frac{{{{\sin }^2}\varphi + {{\cos }^2}\varphi }}{{{\rm{sin}}\varphi \cos \varphi }} = \tan \varphi + \frac{1}{{\tan \varphi }} \equiv R\tan \theta + \frac{1}{{R\tan \theta }}$$
and likewise
$$\frac{1}{{{\rm{sin}}\theta \cos \theta }} = \tan \theta + \frac{1}{{\tan \theta }}$$
whence
$$p = k\left( {R + 1} \right)\left\{ {\tan \theta + \frac{1}{{R\tan \theta }}} \right\}$$
and so to obtain the lowest value of p, pmin, we can minimise this function with respect to tan θ. If we let tan θ = x, then
$$p = k\left( {R + 1} \right)\left\{ {x + \frac{1}{{Rx}}} \right\}$$
and so the function is a minimum when R x2 = 1. Hence,
$$\frac{{{p_{\min }}}}{{2k}} = \frac{{\left( {R + 1} \right)}}{{\sqrt R }}$$
Thus, for this model of extrusion in which there is sliding on the die face, we find:
Extrusion Ratio, R ( = H/h) |
1.33 |
2 |
4 |
10 |
Reduction, r |
25% |
50% |
75% |
90% |
pmin/2k |
2.02 |
2.12 |
2.50 |
3.48 |
0.8 + 1.5 ln R |
0.29 |
0.69 |
1.39 |
2.30 |
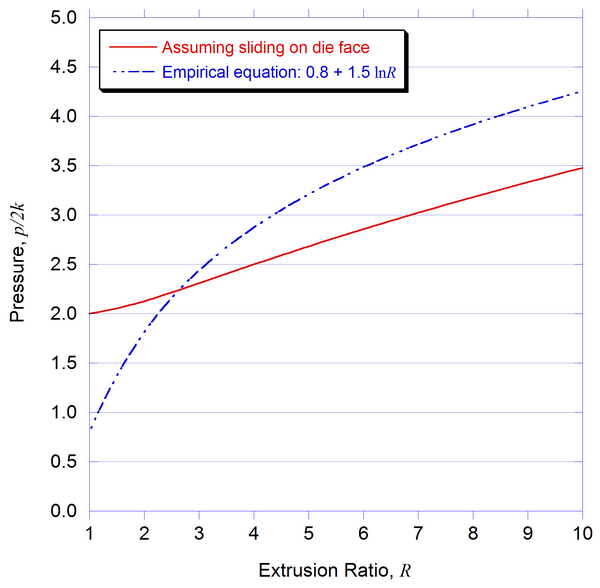
The graph below shows the estimates of p/2k as a function of R, assuming sliding on die face. The empirical equation used in practice 0.8 + 1.5 ln R is plotted for comparison.