• Plane strain
Much deformation of practical interest occurs under a condition that is nearly, if not exactly, one of plane strain, i.e. where one principal strain (say ε3) is zero so that δε3=0.
Plane strain is applicable to rolling, drawing and forging where flow in a particular direction is constrained by the geometry of the machinery, e.g. a well-lubricated die wall.
A specific example of this is in rolling, where the major deformation occurs perpendicular to the roll axis. The material becomes thinner and longer but not wider. Frictional stresses parallel to the rolls (i.e. in the width direction) prevent deformation in this direction and hence a plane strain condition is produced where δε3=0. This can be seen in the animation below.
HOT ROLLING
Reproduced from Materials Selection and Processing CD, by A.M.Lovatt, H.R.Shercliff and P.J.Withers.
![]()
Plastic deformation in plane strain
Here, one principal strain is zero. Let this be ε3. Then δε3= 0.
From the Levy-Mises equation,
\[{{\delta {\varepsilon _1}} \over {{\sigma _1} - {1 \over 2}\left( {{\sigma _2} + {\sigma _3}} \right)}} = {{\delta {\varepsilon _2}} \over {{\sigma _2} - {1 \over 2}\left( {{\sigma _3} + {\sigma _1}} \right)}} = {{\delta {\varepsilon _3}} \over {{\sigma _3} - {1 \over 2}\left( {{\sigma _1} + {\sigma _2}} \right)}} \ne 0\] it follows that \({\sigma _3} = {\textstyle{1 \over 2}}\left( {{\sigma _1} + {\sigma _2}} \right)\) in order to avoid \({{\delta {\varepsilon _1}} \over {{\sigma _1} - {1 \over 2}\left( {{\sigma _2} + {\sigma _3}} \right)}}\) = 0
Hence σ3 is the mean of σ1 and σ2. By convention we define σ1 > σ2 σ1 > σ3 > σ2. Therefore the maximum shear stress in the σ1- σ2 plane is at 45° to the axes and has magnitude \({{{\sigma _1} - {\sigma _2}} \over 2}\) .
If we now examine the Tresca and von Mises yield criteria, we find:
- Tresca \({{{\sigma _1} - {\sigma _2}} \over 2}\) = k = \({Y \over 2}\) (k = shear yield stress and Y = uniaxial yield stress)
- von Mises \({\left( {{\sigma _1} - {\sigma _2}} \right)^2} + {\left( {{\sigma _2} - {\sigma _3}} \right)^2} + {\left( {{\sigma _3} - {\sigma _1}} \right)^2} = 6{k^2} = 2{Y^2}\)
$${\rm{If}\;\;\sigma _3} = {\textstyle{1 \over 2}}\left( {{\sigma _1} + {\sigma _2}} \right),{\rm{ }}{\textstyle{3 \over 2}}{\left( {\sigma {}_1 - {\sigma _2}} \right)^2} = 6{k^2} = 2{Y^2}$$
$$ \Rightarrow \left( {{\sigma _1} - {\sigma _2}} \right) = 2k = {{2Y} \over {\sqrt 3 }}$$
Therefore, if we have plane strain, the Tresca yield criterion and the von Mises yield criterion have the same result expressed in terms of k. It is unnecessary to specify which criterion we are using, provided we use k.
![]()
Consider a metal in uniaxial compression where plastic strain only takes place in the 1-2 plane. There is no friction between the work piece and the die faces. (To achieve this experimentally, a sample should be wide in the 3 direction).
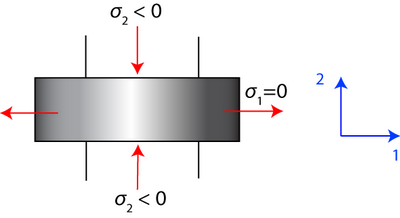 -->
-->
\[ \Rightarrow {\rm{ }}{\sigma _{{\rm{ij}}}} = {\rm{ }}\left( {\matrix{ {{\sigma _1}} & 0 & 0 \cr 0 & {{\sigma _2}} & 0 \cr 0 & 0 & {{{{\sigma _1} + {\sigma _2}} \over 2}} \cr } } \right)\]
Hydrostatic stress:
\[{\sigma _H} = - p = {{{\sigma _1} + {\sigma _2}} \over 2} = {\sigma _3}\]
where p is the hydrostatic pressure.
So at yield, we have \({{{\sigma _1} - {\sigma _2}} \over 2}\) = \(k\) and since \({{{\sigma _1} + {\sigma _2}} \over 2}\) = \(- p\), we have
\[{\sigma _1} = - p + k = 0\]
\[{\sigma _2} = - p - k = - 2k\] since p=k at yield
\[{\sigma _3} = - p\]
So for this example, the stress tensor is
\[{\rm{ }}{\sigma _{{\rm{ij}}}} = {\rm{ }}\left( {\matrix{
{ - p} & 0 & 0 \cr
0 & { - p} & 0 \cr
0 & 0 & { - p} \cr
} } \right) + \left( {\matrix{
k & 0 & 0 \cr
0 & { - k} & 0 \cr
0 & 0 & 0 \cr
} } \right)\]
which is the sum of hydrostatic stress (which can vary in magnitude through the object) and deviatoric pure shear stress (which has the same value throughout the material).
The directions of maximum shear therefore lie at 45° to σ1 and σ2. These are slip lines along which plastic flow occurs.
We are avoiding additional complexities such as work hardening by assuming the materials are rigid-plastic.

