• Plane stress
In plane stress, one of the principal stresses is zero but there are three finite strains. An example of this is the surface of a thin walled, pressurised cylinder, where the principal stress normal to the surface has a value of zero. More generally, plane stress conditions occur in sheet metal forming when a thin sheet is subjected to uniaxial or biaxial tension.
Plastic deformation in plane stress
Consider the uniaxial tensile behaviour of a sheet.
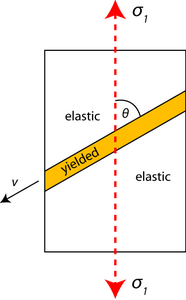
Plastic flow will result once a critical stress is reached. Due to the constraint of neighbouring elastic material, the plastically deforming material forms in a band across the sheet at a characteristic angle to the axis of loading.
\[{\sigma _1} \ne 0{\rm{ , }}{\sigma _{\rm{2}}} = {\sigma _3} = 0\]
At the boundary between the elastic and the yielded material, longitudinal strains must match for continuity. Therefore, they must be zero since strain is effectively zero in the elastic regions.
Plastic strain along v is zero: δεvv= 0
From the Levy-Mises equations \[{{\delta {\varepsilon _1}} \over {{\sigma _1}}} = {{\delta {\varepsilon _2}} \over { - {\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}{\sigma _1}}} = {{\delta {\varepsilon _3}} \over { - {\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}{\sigma _1}}}\], and so \(\delta {\varepsilon _1} = - 2\delta {\varepsilon _2}\) in the plane of the sheet.
Hence if we let δε1= +2 units of plastic strain, δε2= –1 unit of plastic strain.
Therefore, on a Mohr's circle, we have:
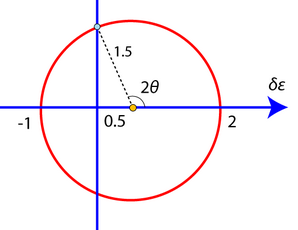
and the longitudinal strain δε is zero, i.e. δεvv= 0, at an angle θ with respect to the direction parallel to σ1.
From the diagram,
\[\cos \left( {180 - 2\theta } \right) = {{0.5} \over {1.5}} = {1 \over 3}\]
\[ \Rightarrow {\rm{ }}\theta = {\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}{\cos ^{ - 1}}\left( { - {\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}}} \right) = {54.74^ \circ }\]
and so the longitudinal strain increment is δεvv = 0 at an angle of with respect to σ1.
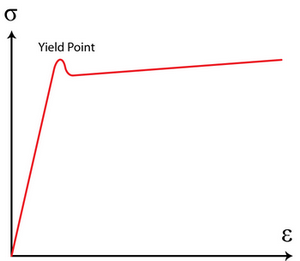
This phenomenon is well known in mild steel. The bands created are known as Lüders bands. These bands require less stress for their propagation than for their formation because of the freeing of dislocations from their solute atmospheres.

(Lüders bands formation in steel, contributed by Mike Meier, University of California, Davis.)
It is worth noting that Lüders bands occur in certain types of steel, such as low carbon steel (mild steel), but not in other metallic alloys, such as aluminium alloys or titanium alloys. This is because plastic strain localisation is normally suppressed by work hardening, which tends to make plastic flow occur rather uniformly in a metal, particularly in the early stages of plastic flow, i.e., just after yield has taken place.
However, in certain types of low carbon steel at room temperature, Cottrell atmospheres of carbon atoms which have been able to segregate preferentially to dislocation cores pin dislocations until the upper yield point is reached. Once the upper yield point is reached, there is a load drop and then a sudden burst of plastic straining at a constant externally applied load, as cascades of dislocations are able escape their Cottrell atmospheres. This is clearly rather specialised behaviour, caused by the ability of carbon atoms to diffuse relatively easily interstitially in these steels, but it is actually necessary behaviour for the formation of Lüders bands.
Conventional work hardening in metallic alloys in the early stages of plastic deformation makes any strain localisation (as demonstrated by the formation of Lüders bands) unlikely. This is also the case for pure metals, and for metals at high temperature, where large plastic strains can occur without a significant load increase once plastic deformation begins.
Therefore, Lüders bands only form if a limited burst of plastic straining is able to take place at constant load. Mild steels heated to sufficiently high temperatures (> 400 °C) and then tensile tested do not exhibit Lüders bands.

