Dissemination of IT for the Promotion of Materials Science (DoITPoMS)

DoITPoMS Teaching & Learning Packages Analysis of Deformation Processes • Notched bar in tension
Analysis of Deformation Processes AimsBefore you startIntroductionLévy-Mises Equations• Plane stress• Plane strainSlip Line Field TheoryWork Formula MethodLimit Analysis• Notched bar in tension• Notched bar in plane bending• Hodographs I• Hodographs IIFinite Element MethodSummaryQuestionsGoing further
TLP creditsTLP contentsShow all content
Viewing and downloading resourcesAbout the TLPsTerms of useFeedbackCredits Print this page
PreviousNext

• Notched bar in tension

The plane strain condition is satisfied when breath, b » h, the depth of the bar.


Lower-Bound:

Find a stress system, e.g. σ = 0 in the length of the bar where there is the notch, σ = 2k elsewhere.


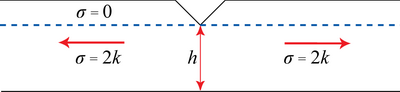
Therefore, for a breadth b, P = 2khb = load = stress × area


Upper-Bound:

Postulate a suitable simple deformation pattern.


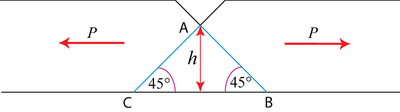
Assume yielding by slip on 45º shear planes with shear yield stress k. Let displacement along shear plane AB = δx.

Then internal work done = \( {k.\left| {AB} \right|b\delta x} = k\sqrt 2 bh\delta x\), where the force is \( k\left| {AB} \right|b \) acting on the shear plane AB.

Distance moved by the external load \(P = \delta x\cos {45^ \circ }\) = \(\frac{{\delta x}}{{\sqrt 2 }}\)

\( \Rightarrow P \) \(\frac{{\delta x}}{{\sqrt 2 }}\) = \(k\sqrt 2 bh\delta x\)

\( \Rightarrow P = 2kbh\)


So, here we obtain the same result for the upper bound and lower bound \( \Rightarrow P = 2kbh\) is the true failure load, the load required to cause plastic flow.

 

PreviousNext