Extrusion: assuming dead metal zone at 45°

The mathematics behind the equation for p_min:

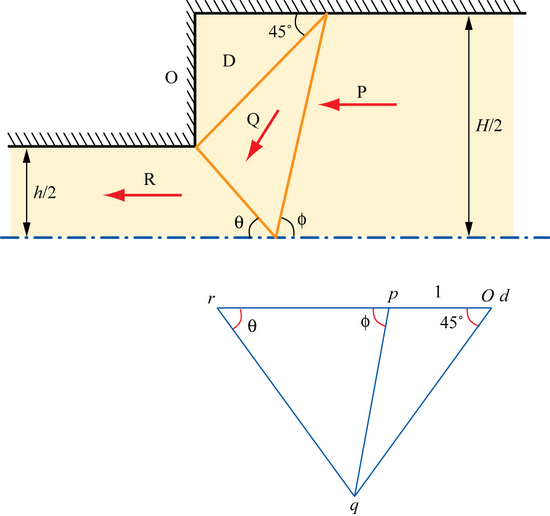
Mathematically, this is more complicated than the situation in which there is sliding on the die face.

In the hodograph, it is convenient to define angle Orq in the hodograph as θ and angle rpq as φ. By definition, angle pOq is 45°.

Applying the general formula

$$pa = k\sum\limits_n {\left| {{\rm{SS}}{'_n}} \right|} \left| {{v_{sn}}} \right|$$

we then have

\[p\frac{H}{2} = k\left\{ {{\rm{PQ}}{v_{pq}} + {\rm{DQ}}{v_{dq}} + {\rm{QR}}{v_{qr}}} \right\}\]

where PQ is the length of the line dividing regions P and Q, DQ is the length of line dividing regions D and Q and QR is the length of line dividing regions Q and R in the above diagram showing the extrusion operation.

Now,

$${\rm{PQ}} = \frac{H}{{2\sin \varphi }}{\rm{ , DQ}} = \frac{1}{{\sqrt 2 }}\left( {H - h} \right){\rm{ \;\; and\;\; QR}} = \frac{h}{{2\sin \theta }}$$

In the hodograph, Op = 1 and Or = R, the extrusion ratio, i.e., ν_Op = 1 and ν_Or = R.

From triangle Opq, we having, using the sine rule,

\[\frac{{pq}}{{\sin {{45}^ \circ }}} = \frac{1}{{\sin \left( {\phi - {{45}^ \circ }} \right)}},{\rm{ \;\; and \;\;so \;\; }}{v_{pq}} = \frac{1}{{\sin \phi - \cos \phi }}\]

Likewise,

\[\frac{{dq}}{{\sin \left( {{{180}^ \circ } - \phi } \right)}} = \frac{1}{{\sin \left( {\phi - {{45}^ \circ }} \right)}},{\rm{ \;\; and \;\;so \;\; }}{v_{dq}} = \frac{{\sqrt 2 \sin \phi }}{{\sin \phi - \cos \phi }}\]

Finally, in triangle pqr, we find

\[\frac{{pq}}{{\sin {\rm{\theta }}}} = \frac{{qr}}{{\sin \phi }},{\rm{ \;\; and \;\;so \;\; }}{v_{qr}} = \frac{{\sin \phi }}{{\left( {\sin \phi - \cos \phi } \right)}}.\frac{1}{{\sin {\rm{\theta }}}}\]

Hence,

$$p\frac{H}{2} = k\left\{ {\frac{{\rm{1}}}{{\left( {{\rm{sin}}\varphi {\rm{ - cos}}\varphi } \right)}}.\frac{H}{{2\sin \varphi }} + \frac{{\left( {H - h} \right)\sin \varphi }}{{\left( {{\rm{sin}}\varphi {\rm{ - cos}}\varphi } \right)}} + \frac{{{\rm{sin}}\varphi }}{{\left( {{\rm{sin}}\varphi {\rm{ - cos}}\varphi } \right)}}.\frac{h}{{2{{\sin }^2}\theta }}} \right\}$$

We can eliminate θ from this expression by observing from the diagram of the extrusion operation that

$$\frac{h}{{2\tan \theta }} + \frac{H}{{2\tan \varphi }} = \frac{H}{2} - \frac{h}{2},{\rm{ i}}{\rm{.e}}{\rm{., }}\frac{1}{{\tan \theta }} + \frac{R}{{\tan \varphi }} = R - 1$$

Rearranging our expression for p, we have

\[pR = \frac{k}{{\left( {{\rm{sin}}\phi {\rm{ - cos}}\phi } \right)}}\left\{ {\frac{R}{{\sin \phi }} + \sin \phi \left( {2R - 2 + \frac{1}{{{{\sin }^2}\theta }}} \right)} \right\} = \frac{k}{{\left( {{\rm{sin}}\phi {\rm{ - cos}}\phi } \right)}}\left\{ {\frac{R}{{\sin \phi }} + \sin \phi \left( {2R - 1 + {{\cot }^2}\theta } \right)} \right\}\] \[{\rm{ }} = \frac{k}{{\left( {{\rm{sin}}\phi {\rm{ - cos}}\phi } \right)}}\left\{ {\frac{R}{{\sin \phi }} + \sin \phi \left( {2R - 1 + {{\left( {R - 1 - R\cot \phi } \right)}^2}} \right)} \right\}\] \[{\rm{ }} = \frac{{kR}}{{\left( {{\rm{sin}}\phi {\rm{ - cos}}\phi } \right)}}\left\{ {\frac{{R + 1}}{{\sin \phi }} - 2\left( {R - 1} \right)\cos \phi } \right\}{\rm{ \;\; after\;\; some\;\; algebra}} \]

Hence,

$$\frac{p}{{2k}} = \frac{1}{{2\left( {{\rm{sin}}\varphi {\rm{ - cos}}\varphi } \right)}}\left\{ {\frac{{R + 1}}{{\sin \varphi }} - 2\left( {R - 1} \right)\cos \varphi } \right\}$$

To find the minimum value of p, we have to minimise the right hand side with respect to φ. This occurs at the angle of φ defined by the expression

$$\cot \varphi = 1 - \frac{2}{{\sqrt {R + 1} }}$$

whence after some more algebra, we find

$$\frac{{{p_{\min }}}}{{2k}} = 2\left( {\sqrt {R + 1} - 1} \right)$$

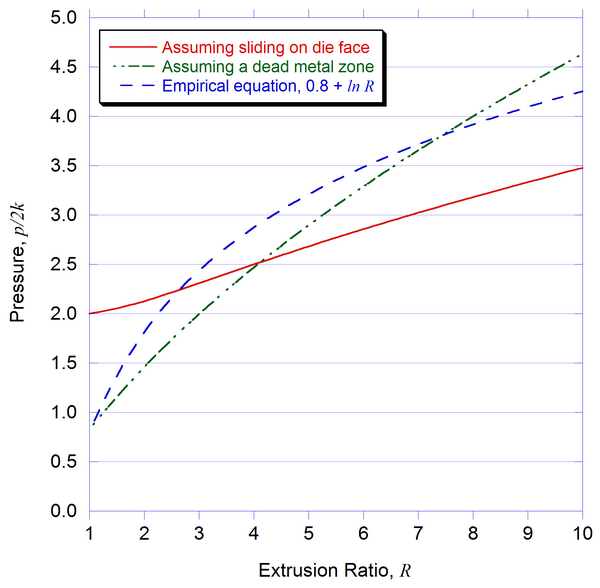
The plot below shows the estimates of p/2k as a function of R, comparing:

• extrusion model assuming sliding on die face
• extrusion model assuming dead metal zone at 45°
• empirical relation used in practice 0.8 + 1.5 ln R