Dissemination of IT for the Promotion of Materials Science (DoITPoMS)

DoITPoMS Teaching & Learning Packages Finite Element Method Introduction
Finite Element Method AimsBefore you startIntroductionNodes, elements, degrees of freedom and boundary conditionsDirect stiffness method and the global stiffness matrixEnforcing Boundary ConditionsInterpolation/Basis/Shape Functions1D first order shape functions1D second order shape functionsTypical steps during FEM modellingSummaryQuestions
TLP creditsTLP contentsShow all content
Viewing and downloading resourcesAbout the TLPsTerms of useFeedbackCredits Print this page
PreviousNext

Introduction

Overview

The Finite Element Method (FEM) is a mathematical (numerical) technique for finding approximate solutions to partial differential equations. It is a technique which is very well suited to the study and analysis of complex physical phenomena, particularly those exhibiting non-linearity in geometry and/or material behaviour (which is often the case for most “real-world” situations). It is used frequently to tackle problems that are not readily amenable to analytical treatments. Such problems can be structural, thermal, electrical, magnetic, acoustic etc., either in isolation or when coupled. Coupled examples include (but are not limited to) thermomechanical – where constrained differential thermal expansion generates thermal-stresses, thermoelectric – where heat is generated in a material due to its resistance to current flow, and conjugate heat transfer – where moving fluids can remove heat from hot objects over which they pass. When the Finite Element Method is used to solve problems of this type it is often referred to as Finite Element Analysis (FEA).

Premise

The premise is very simple; continuous domains (geometries) are decomposed into discrete, connected regions (or Finite Elements). An assembly of element-level equations is subsequently solved, while conditions of kinematic compatibility are enforced, in order to establish the response of the complete domain to a particular set of boundary conditions. The premise is described to some degree in the figure below, which also lists the governing equations (in differential form) for a range of common physical phenomena (in 1-D).

discretisation of continuous domains

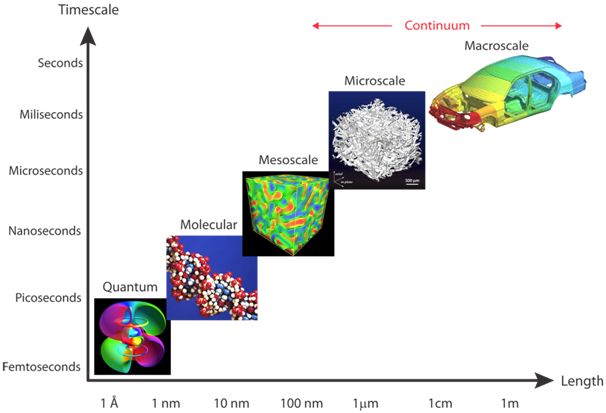
Time and Lengthscales

Typical time and lengthscales for application of the finite element method are shown in the following figure.

Time and lengthscales for application of FEM

Example Videos:

The videos below have been produced from finite element analyses and include:

FEM of plate perforation

Punch

PreviousNext