Dissemination of IT for the Promotion of Materials Science (DoITPoMS)

DoITPoMS Teaching & Learning Packages Fuel Cells • Thermodynamics
Fuel Cells AimsBefore you startIntroductionThe principleHistory of the technologyTypes of fuel cellsSolid oxide fuel cells (SOFCs)• Electrolyte• Electrode materials• Interconnection• Thermodynamics• System and outlookMolten carbonate fuel cells (MCFCs)• Electrolyte• Electrochemistry• ElectrodesProton exchange membrane fuel cells (PEMFCs)• Membrane• Electrodes and membrane-electrode assembly• Efficiency and reaction conditionsFuelling requirementsCase study: Fuelling practicalitiesSummaryQuestionsGoing further
TLP creditsTLP contentsShow all content
Viewing and downloading resourcesAbout the TLPsTerms of useFeedbackCredits Print this page
PreviousNext

• Thermodynamics

A SOFC is an electrochemical device that converts chemical energy of the fuel and oxidant directly and reversibly into electrical energy. They are not a better or improved heat engine, they are fundamentally different. Hydrogen and oxygen are going to be used to illustrate the thermodynamics of the fuel cell.


The ideal reversible SOFC – Basic derivation of potential and efficiency

The first and second law of thermodynamics describe the reversible SOFC. The reactants (fuel and air) deliver total enthalpy \(\sum {{n_i}{H_i}} \) and the total enthalpy \(\sum {{n_j}{H_j}} \) leaves the fuel cell, so the change in enthalpy, ΔH = \(\sum {{n_j}{H_j}} \) –  \(\sum {{n_i}{H_i}} \). The heat qFC has to be extracted from the fuel cell and the reversible work wFC delivered.



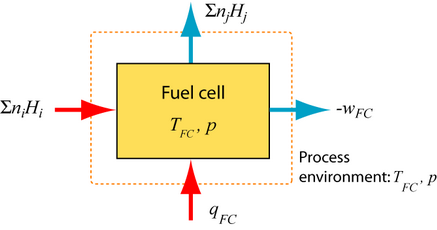
1st Law of thermodynamics: \({q_{FC}} + {w_{FC}} = \Delta H\)

2nd Law of thermodynamics: \(\oint {dS = 0} \)

The reaction entropy has to be compensated by the transport of heat to the environment: \(\Delta S - \) \({{{q_{FC}}} \over {{T_{FC}}}} \)\( = 0\)

The reversible work is from the above equations: \({w_{FC}} = \Delta H - {T_{FC}} \cdot \Delta S\)

The Gibbs enthalpy is equal to the reversible work of the reaction. The reversible efficiency is equal to the ratio of the Gibbs and the reaction enthalpy:

$${\eta _{FC}} = {{\Delta G} \over {\Delta H}} = {{\Delta H - {T_{FC}} \cdot \Delta S} \over {\Delta H}}$$


The fuel cell is an electrical device, for which the processes can be fully described by thermodynamic principles.

Hydrogen is absorbed at the anode, it is ionized and the electrons are conducted away to do useful work. Oxygen atoms that arrive at the cathode are ionized by the electrons coming from the anode. The protons and oxide ions react and form water.

Anode: H2 ↔ 2H+ + 2e–
Cathode: ½O2 + 2e–↔ O2–
The net reaction is: 2H+ + O2– ↔ H2O

This shows that the molar flow of hydrogen is twice the molar flow of oxygen. The electric current is therefore:

$$I = {\dot n_{el}} \cdot \left( { - e} \right) \cdot {N_A} = - 2{\dot n_{{H_2}}} \cdot F$$




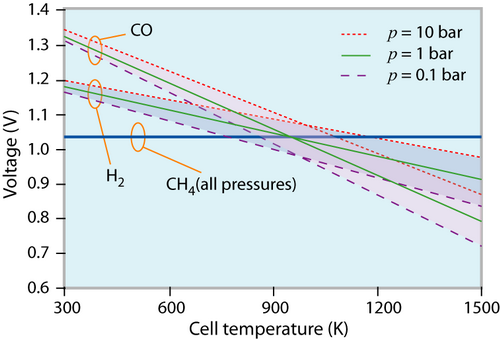
The reversible cell voltage of different fuels at different states (p, T) of the environment

 

The electric current is a measure of the rate at which fuel is spent. The electric and thermodynamic quantities are matched by considering reversible power:

$$P = V \cdot I = {\dot n_{{H_2}}} \cdot w = {\dot n_{{H_2}}} \cdot \Delta G$$

Hence the reversible voltage:

$$V = {{ - {{\dot n}_{{H_2}}} \cdot \Delta G} \over {{{\dot n}_{el}} \cdot F}} = {{ - \Delta G} \over {{{\dot n}_{el}} \cdot F}}$$

Using the assumption that we have (near) ideal gases, a more accurate equation for the Gibbs energy is:

$$\Delta G(T,p) = \Delta H(T) - T \cdot \Delta S(T,p)$$

where

$$S(T,p) = {S^0} + \int\limits_{{T_0}}^T {{{{C_p}(T)} \over t}dt} - R \cdot \ln ({p \over {{p_0}}})$$

We get for the Gibbs energy:

$$\Delta G(T,p) = \Delta G(T) + T \cdot R \cdot \ln (K)$$

where K is the equilibrium constant.

We get from the above analysis the Nernst potential:

$${V_N} = {{ - \Delta G(T)} \over {{n_{el}} \cdot F}} - {{R \cdot T \cdot \ln (K)} \over {{n_{el}} \cdot F}}$$

 

 Going further: The chemical thermodynamics of SOFCs.

 

PreviousNext