Fuel Cells (all content)
Note: DoITPoMS Teaching and Learning Packages are intended to be used interactively at a computer! This print-friendly version of the TLP is provided for convenience, but does not display all the content of the TLP. For example, any video clips and answers to questions are missing. The formatting (page breaks, etc) of the printed version is unpredictable and highly dependent on your browser.
Contents
Main pages
Additional pages
Aims
On completion of this TLP, the student should gain an understanding of the following topics of discussion:
- The principle behind fuel cells and what constitutes a fuel cell.
- A brief history of the technology.
- Function and specifics of four main types of fuel cell:
- Solid oxide fuel cell (SOFC)
- Molten carbonate fuel cell (MCFC)
- Proton exchange membrane/ polymer electrolyte membrane fuel cell (PEMFC)
- Direct methanol fuel cell (DMFC)
- The advantages, problems and applications associated with each of the different electrolytes commonly used in fuel cells, including discussion of the factors influencing their suitability.
- The electrochemical explanation of the fuel cell processes.
- The requirements of fuelling a fuel cell system including “balance of plant” considerations, reforming and ways of storing the fuel.
- Building a simple fuel cell.
Before you start
- You should be familiar with the principles of electrochemical reactions
- You should understand the principles of thermodynamics
Introduction
Conventional power plants convert chemical energy into electrical energy in three steps:
- Production of heat by burning fuel
- Conversion of heat into mechanical energy
- Conversion of mechanical energy into electrical energy
The efficiency of the second step is limited (by the Second Law of Thermodynamics) to the Carnot efficiency, since the conversion of heat into mechanical energy occurs in a closed-cycle heat engine. An efficiency of about 41% can be reached by modern systems. A fuel cell is an electrochemical device that converts the chemical energy in fuels (e.g. hydrogen, methane, butane or even gasoline and diesel) into electrical energy. It exploits the natural tendency of oxygen and hydrogen to react to form water. The direct reaction is prevented by the electrolyte, which separates the two reactants. Therefore two half-reactions occur at the electrodes:
|
The ions are transported to the other electrode through the electrolyte. The fuel cell contains no moving parts and only four active elements: cathode, anode, electrolyte and interconnect; it is a simple and robust system. Fuel cells have a number of advantages compared to conventional electricity generation:
- Negligible air pollution (if fossil fuels are used, otherwise none)
- Reduced weight, especially in mobile applications
- 100% theoretical efficiency, 80% efficiency in high temperature turbine hybrid systems, that can use the generated heat
High efficiency in low power systems
- Constant efficiency at low load
- Flexible output with fast adjustment
- Low maintenance cost and very few moving parts (or none)
- Quiet or completely silent
Fuel cells have many interesting applications. This short video shows a demonstration fuel cell car. Note that hydrogen and oxygen being used up by the reactions.
The principle
Oxygen and hydrogen, when mixed together in the presence of enough activation energy have a natural tendency to react and form water, because the Gibbs free energy of H2O is smaller than that of the sum of H2 and ½O2 added together (Hence, we don’t smoke our pipes on Zeppelins!). If hydrogen and oxygen were combined directly, we would see combustion:
H2 + ½O2 → H2O |
Combustion involves the direct reaction of H2 gas with O2. The hydrogen donates electrons to the oxygen . We say that the oxygen has been reduced and the fuel oxidised. This combustion reaction releases heat energy.
The fuel cell separates hydrogen and oxygen with a gas-impermeable electrolyte through which only ions (e.g. H+, O2-, CO32–) can migrate. Hence two half reactions occur at the two electrodes. The type of reactions at the electrodes is determined by the type of electrolyte.
Grove’s fuel cell is one of the simplest examples.
The half-reaction at the anode: The half-reaction at the cathode: The net reaction is the combustion reaction: |
Activation polarization is caused by the energy intensive activity of the making and breaking of chemical bonds: At the anode, the hydrogen molecules enter the reaction sites so that they are broken into ions and electrons. The resulting ions form bonds with the catalyst atoms and the electrons remain in the vicinity until new hydrogen molecules start bonding with the catalyst, breaking the bond between the earlier ion. The electrons migrate through the bipolar plate if the bonding energy of the ion is low enough and the ions diffuse through the electrolyte. A similar process occurs at the cathode: Oxygen molecules are broken up and react with the electrons from the anode and the protons that diffused through the electrolyte to form water. Water is then ejected as a waste product and the fuel cell runs (can supply a current), as long as fuel and oxygen is provided.
The exact reactions at the electrodes depend upon which species can be transported across the electrolyte. Fuel cells are classified according to the type of electrolyte (see Types of Fuel Cells). The most common electrolytes are permeable for protons and the reactions are as discussed above. The second most common electrolytes, found in solid oxide fuel cells (SOFCs), are permeable for oxide ions and the following half-reactions occur:
The half-reaction at the anode: The half-reaction at the cathode: |
A third type of electrolyte, used for molten carbonate fuel cells at high temperatures conducts carbide ions (CO32–):
The half-reaction at the anode: The half-reaction at the cathode: The net reaction is the combustion reaction: |
We also commonly see alkaline electrolytes, across which OH– is the transported species. In this case the half-reactions would be:
The half-reaction at the anode: The half-reaction at the cathode: The net reaction is the combustion reaction: |
![]()
 Building a simple fuel cell
Building a simple fuel cell
![]()
History of the technology
The fuel cell concept was first demonstrated by William R. Grove, a British physicist, in 1839. The cell he demonstrated was very simple, probably resembling this:
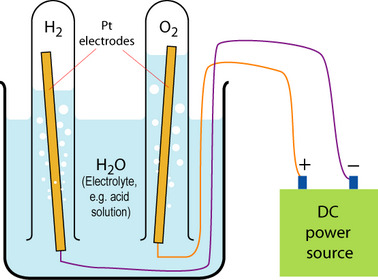 Electrolysis setup
Electrolysis setup
By application of a voltage across the two electrodes, hydrogen and oxygen could be extracted (the process is called electrolysis) and captured as shown (William Nicholson first discovered this in 1800). The fuel cell, or “gas battery” as it was first known, is the reverse of this process. In the presence of platinum electrodes, which are necessary as catalysts, the electrolysis will essentially run in reverse and current can be made to flow through a circuit between the two electrodes.
Nobody tried to make use of the concept demonstrated by William R Grove until 1889 when Langer and Mond tried to engineer a practical cell fuelled by coal gas. Further early attempts carried on into the early 1900’s but the development of the internal combustion engine made further research into the technology sadly unnecessary.
Francis Bacon developed the first successful fuel cell in 1932, running on pure O2 and H2 and using an alkaline catalyst and nickel electrodes. It was not until 1959 that Bacon and his colleagues first demonstrated a 5 kW device; the 27 year delay is perhaps an indication of just how difficult it is to make progress in this field of development. Harry Karl Ihrig demonstrated a 20 bhp fuel cell tractor in the same year.
Around about this time, NASA started researching the technology with a view to produce a compact electricity generator for use on spacecraft. Due to their astronomical budget, it was not long before they got the job done. The Gemini program used early PEM fuel cells (PEMFCs) in its later missions, and the Apollo program employed alkaline fuel cells. On a spacecraft the water produced by the reaction was available for the spacemen to drink. NASA continued to use alkaline cells in the space shuttle until the 90’s when PEMFC development meant a switch back to PEMs was considered a possibility, however, the high cost of design, development, test and evaluation prevented the switch, in spite of several technical advantages.

PEM fuel cells being installed in a Gemini 7 spacecraft (Source: Smithsonian Institution, from the Science Service Historical Images Collection, courtesy of General Electric)

The alkaline fuel cell system as used on the space shuttles. Three such modules were installed in each shuttle
Recent developments are thick and fast as the technology begins to come to fruition. Automotive applications are high on the agenda due to the huge consumer market and the need for an environmentally friendly, renewable alternative to the internal combustion engine and fossil fuels.

Honda fuel cell car
DoITPoMS standard terms of use
Types of fuel cells
Fuel cells are categorised according to their type of electrolyte, since it is the property-determining component. The six main types of fuel cells are outlined below.
Fuel cell type |
DMFC |
AFC |
PAFC |
|||
Electrolyte type |
Polymeric ion exchange membrane |
Polymeric ion exchange membrane |
Immobilised alkaline salt solution |
Immobilised liquid phosphoric acid |
Immobilised liquid molten carbonate |
Ceramic |
Operating temperature (°C) |
20 – 90 |
30 – 100 |
50 – 200 |
~220 |
~650 |
500 – 1000 |
Charge carrier |
H+ |
H+ |
OH– |
H+ |
H32– |
O2– |
Power range (W) |
1 – 100 |
1 – 100k |
500 – 10k |
10k – 1M |
100k – 10M+ |
1k – 10M+ |
Applications and main advantages: |
||||||
Portable electronics |
Higher energy density than batteries and faster recharge. |
|
|
|
|
|
Cars boats and spaceships |
|
Zero emissions and higher efficiency. |
|
|
|
|
Domestic CHP |
|
|
Efficiency and reliability |
|
|
|
Distributed power generation, CHP, busses |
|
|
|
|
Efficiency, emissions and less noise |
|
Able to internally reform CH4 |
× |
× |
× |
× |
√ |
√ |
The phosphoric acid fuel cell (PAFC) is not covered in detail in this package. It was however the first type of fuel cell to be commercially produced and enjoys widespread terrestrial use. Many 200 kW systems are in place in USA and Europe.
This package also doesn’t cover the alkaline fuel cell (AFC) in any detail. These particular cells use potassium hydroxide solution as the electrolyte. This means that any CO2 at the cathode, even the levels present in the air, will react with the OH– in the solution to produce carbonates and prevent the cell functioning. This isn’t a huge problem in spacecraft, where pure oxygen can be supplied to the cathode reliably, but this characteristic flaw makes the AFC unsuitable for practical terrestrial use.
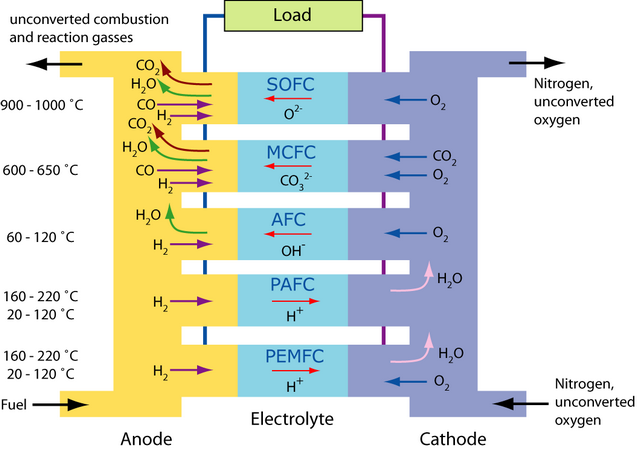
The diagram below shows the mechanisms by which the different fuel cell types operate:
![]()
 Other types of fuel cells?
Other types of fuel cells?
![]()
What’s the catch?
As fossil fuel resources become more and more pressed upon to deliver the worlds energy needs, as CO2 and global warming loom ever nearer and as cities become ever increasingly crowded with polluting automobiles the fuel cell seems to offer a golden solution to the world's energy problems. It’s efficient, it’s clean, hydrogen can be produced by renewable energy and the technology wouldn’t require any huge change in our way of life.
So why don’t we all drive fuel cell cars already? The technology has two fundamental flaws:
- Slow reaction rate, leading to low currents and power.
- Hydrogen is not a readily available, or easily stored fuel.
We’ll discuss ways of getting around these problems in the package. Each type of fuel cell has a different solution, but also brings its own set of difficulties.
![]()
Temperature differences
High temperature cells (solid oxide and molten carbonate electrolytes) operate by very different mechanisms to low temperature cells, and have different applications accordingly. The requirements of the “balance of plant” (i.e. the additional fuel processing equipment necessary to fuel a fuel cell) are also different. We therefore split the TLP in two and consider high temperature cells separately from low temperature cells.
Solid oxide fuel cells (SOFCs)
High temperature cells
In the late nineteenth century, conduction was not yet understood. Later, Nernst observed at the University of Göttingen, that stabilized zirconia (ZrO2 doped with Ca, Mg, Y) was an insulator at room temperature, an ionic conductor from 600–1000 °C and a mixed conductor (both electronic and ionic) at around 1500 °C. The main part of the solid oxide fuel cell was therefore discovered. The fuel cell concept was demonstrated by Baur and Preis in the 1930’s using zirconium oxide, but many improvements were necessary to make a competitive device. In the 1950’s, simple, straightforward design made cheaper manufacturing processes possible: the flat plate fuel cell.
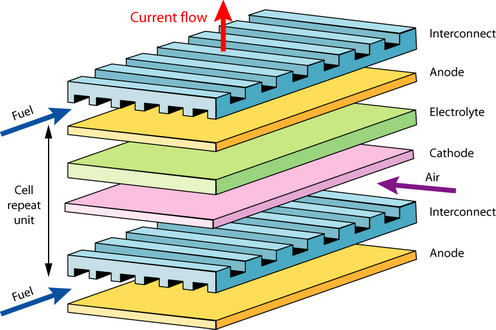
Flat plate solid oxide fuel cell
There are a few problems with the flat plate design when used for larger devices: sealing, around the edges, thermal expansion mismatch and cracking (intrinsically brittle ceramics are used). Tubular designs have been developed to solve these problems (see animation below).
SOFCs are the most efficient devices yet invented, that can convert chemical energy into electrical energy. Both electrodes (cathode and anode) and the electrolyte are made of ceramic materials, since the high operating temperature prevent the use of cheaper metals. The big advantage of the SOFC over the MCFC is that the electrolyte is solid and there are no pumps required to circulate the hot electrolyte. The anode contains nickel, for better electron conduction and catalysis. The operating temperature is between 600 and 1000 °C, depending on the generation of the fuel cell (first, second and third, with decreasing operating temperature). However, thermal cycling can cause cracking of the brittle ceramic components. Both hydrogen and carbon monoxide serve as fuels. Common hydrocarbon fuels can be used in SOFC (diesel, natural gas, gasoline, alcohol etc).
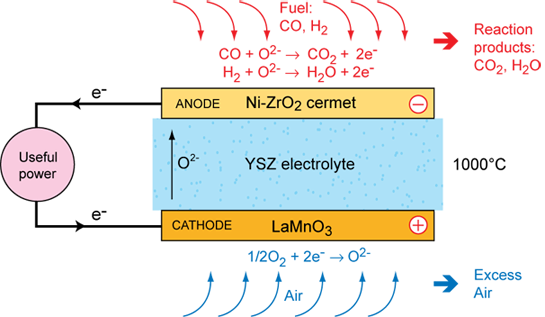
Operation of a SOFC
The operation of the solid oxide fuel cell is straightforward: oxygen atoms are reduced on the porous cathode surface by electrons. The oxide ions diffuse through the electrolyte to the fuel rich and porous anode, where they react with the fuel (hydrogen) and give off electrons to an external circuit. A large amount of heat is produced by the electrochemical reaction, which can be used by an integrated heat management system. Since it takes a long time to reach its operating temperature, the best applications for SOFCs are ones that use both the heat and electricity generated: stationary power plants, auxiliary power supplies. Start-up time problems could be solved by using supercapacitor batteries for the first few minutes of operation in mobile applications.
• Electrolyte
This section of the TLP describes the fundamental properties of the most common materials used as electrolytes in SOFCs.
There are several criteria that the electrolyte has to meet. It must be:
- Dense and leak tight
- Stable in reducing and oxidising environments
- A good ionic conductor at operating temperatures
- Non-electron conductor
- Thin to reduce ionic resistance
- Extended in area for maximum current capacity
- Thermal shock resistant
- Economically processable
The materials used, are solid, ion-conducting ceramics. There are two main groups of such ion conductors: fluorite structured and perovskite structured, besides new materials such as hexagonal structured oxides. The three most common electrolyte materials are: doped ceria (CeO2), doped lanthanum gallate (LaGaO3) (both are oxygen ion conductors) and doped barium zirconate (BaZrO3) (a proton conductor). The concentration and type (ionic radius) of the dopants influence the material properties strongly. Dopants, that cause the least strain and hence the least influence on the potential energy landscape of the parent lattice, have the biggest effect on the conductivity.
In an oxide ion conductor, current flows by the movement of oxide ions through the crystal lattice. This is a thermally activated process, where the ions hop from one lattice site to the other (from one potential valley to the other) in a random way. When an electric field is applied, there is a drift in one direction superimposed on the random thermal motion.
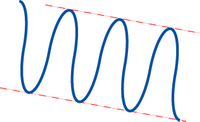
Potential energy in an electric field in a periodic crystal
Ionic conduction depends on the mobility of the ions and therefore on temperature. At high temperatures, the conductivity can reach 1 S cm-1, which is of the same order of magnitude as for liquid electrolytes. The crystal has to contain unoccupied sites that are equivalent to the occupied sites by lattice oxygen ions. The energy barrier for migration from an occupied site to an unoccupied site must be small (≤1 eV). This might seem unusual since the relative size of the oxygen ions is big and it seems more likely that the smaller metal ions migrate in an electric field. That is why there are only a few special structures that make oxygen ion migration possible: fluorite structured oxides, perovskites, LAMOX family and BIMEVOXes.
Fluorite oxides are the most common and classical oxygen ion conducting materials. The crystal structure consists of a cubic oxygen lattice with alternate body centres occupied by eight coordinated cations. The cations are arranged into a face centred cubic structure with the anions occupying the tetrahedral sites. This leaves a rather open structure with large octahedral interstitial void.
Rotating zirconia lattice
DoITPoMS standard terms of use
The general formula has the form AO2, where A is usually a big tetravalent cation, e.g. U, Th, Ce. Since Zr4+ is too small to sustain the fluorite structure at low temperatures, it has to be partly substituted with a larger cation, called dopant. Doping involves usually substituting lower valence cations into the lattice. In order to maintain charge neutrality oxygen vacancies have to be introduced, which allow oxygen ion migration.
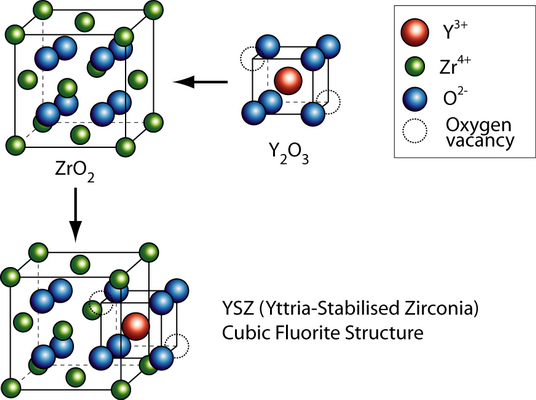
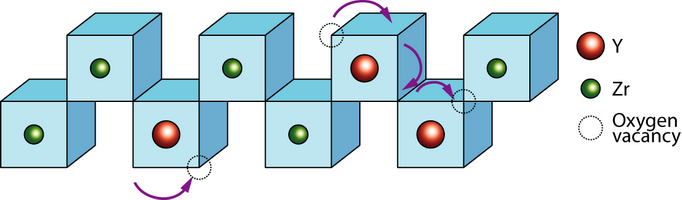
Vacancy transport in YSZ
An interesting feature of the fluorite structure is that it can sustain a high degree of substitution. A very disordered and open structured material results from this, which promotes ionic conduction.

High resolution transmission electron micrograph depicting the nickel and YSZ interface (Image courtesy of Technical University of Tokyo)
By substituting the host cation sites with either rare earth or an alkaline earth element, just as with yttria-stabilised zirconia (YSZ), an increase of ionic conduction can be achieved. Zirconia (zirconium dioxide, ZrO2) in its pure form has a high melting temperature and a low thermal conductivity. The applications of pure zirconia are restricted because it shows polymorphism. It is monoclinic at room temperature and changes to the denser tetragonal phase from circa 1000 °C. This involves a large change in the volume and causes extensive cracking. Hence zirconia has a low thermal shock resistivity. The addition of some oxides results in stabilising the cubic phase and the creation of one oxygen vacancy, i.e. \(2[{\rm{Y}}{'_{{\rm{Zr}}}}] = [{{\rm{V}}_{{{\rm{O}}^{..}}}}]\)
Y2O3(ZrO2) → 2Y’Zr + 3Oxo + Vo
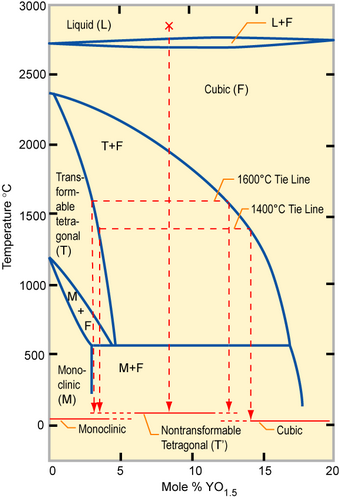
Phase diagram of partially stabilized zirconia (PSZ)
Partially stabilized zirconia (PSZ) is a mixture of zirconia polymorphs: a cubic and a metastable tetragonal ZrO2 phase is obtained, since an insufficient amount of stabilizer has been added. PSZ is also called tetragonal zirconia polycrystal: TZP. PSZ is a transformation-toughened material since the induced microcracks and stress fields absorb energy. PSZ is used for crucibles because it has a low thermal conductivity and a high melting temperature. The addition of 16 mol% CaO or 16 mol% MgO or 8 mol% Y2O3 (8YSZ) is enough to form fully stabilized zirconia. The structure becomes cubic solid solution, which has no phase transformation when heating from room temperature up to 2500 °C. Because of its high oxide ion conductivity, YSZ is often used for oxygen sensoring and solid oxide fuel cells.

Scanning electron micrograph showing 8 mol% Y2O3 (8YSZ) surface (Image courtesy of Altair Nanotechnologies, Inc)
It might be expected that an increase of the dopant concentration would lead to an increase of conductivity. This correlation only applies to low dopant concentrations because at higher levels, the first and second electron coordination shells dopants start interacting with the oxygen vacancies and the conductivity decreases. The conductivity can be calculated as follows:
$$\sigma = {A \over T}\left[ {{{\rm{V}}_{{{\rm{O}}^{..}}}}} \right]\left[ {{{{\rm{\bar V}}}_{{{\rm{O}}^{..}}}}} \right]\exp \left( {{{ - E} \over {RT}}} \right)$$ where E is the activation energy for conduction, T is the temperature, R and A are constants \(\left[ {{{{\rm{\bar V}}}_{{{\rm{O}}^{..}}}}} \right]\) is an unoccupied oxygen vacancy.

Conductivity as a function of temperature, data taken from Ref.[3].
In present fuel cells, the electrolyte of choice is zirconia, stabilised by either 3 mol% Y2O3 (3YSZ) or 8 mol% Y2O3 (8YSZ). YSZ is not the best ion conductor, but it is the cheapest to process and has low enough electronic conductivity. There are many other materials that conduct oxides but the advantages of YSZ: abundance, chemical stability, non-toxicity and economics make it the most suitable material at present. Drawbacks are high thermal expansion coefficient and hence problems with sealing the fuel cell. The world demand for YSZ is rising, but luckily, Zr is one of the most common elements of the Earth’s crust usually in the form of silicate zircon (ZrSiO4). This material has to be purified since SiO2 tends to block the ionic and electron paths.
Yttria is the main stabilizer used and about 13-16 wt% have to be added to give a fully stabilized cubic material. More rare dopants’ supply such as scandia could present a problem in the future.
Another interesting fluorite structured material is CeO2 doped with 10 mol% GdO (GCO). It is especially useful for lower temperature applications. But GCO is an electron conductor in the reducing environment at the anode and hence short-circuiting is a problem.
Fabrication of zirconia electrolyte films is usually done by tape casting or vapour deposition.
The second highly interesting group of solid state ion conductors is perovskites. The general perovskite stoichiometry is ABO3.
Rotating perovskite lattice
DoITPoMS standard terms of use
Due to the number of combinations (2+4, 5+1, 3+3) to have the total charge of +6 on AB, the high stability of the structure and the wide variety of cations that can be accommodated within, perovskites have a wide range of properties, which are suitable not only for SOFCs but also as ferroelectrics, oxidation catalysts or superconductors. High ionic conductivity in perovskites is achieved by doping the material with trivalent elements, such as Y on the Zr site of BaZrO3 for example, so that oxygen vacancies are introduced. The conductivity of ABO3 perovskites strongly depends on the size of the A and less so on the size of the B cation, since the oxides have to migrate through a triangular space, consisting of two large A cations and one smaller B cation. The enlargement of this triangular space facilitates the migration of oxide ions through the lattice. Hence we can expect higher ion conductivity with larger lattice dimensions.
In order to incorporate hydroxyl groups into onto the vacant oxide sites, the material is exposed to humid atmospheres. The second proton of the water molecule attaches to some other oxygen atom in the structure. Due to the loose bonding between the hydrogen ion and the oxygen atom, conduction occurs easily, by hydrogen ions jumping from one oxygen to the other.
The perovskites LaGaO3 and BaZrO3 proved to be highly interesting since their structure is very tolerant and can accommodate large concentrations of dopants but less than in YSZ (hence the ion conductivity of perovskites is always less than that of YSZ).
A particular composition: La0.9Sr0.1Ga0.8Mg0.2O3-d (LSGM) has been found to have similar, purely ionic conductivities to CeO2, also at low temperatures (<600 °C). The evaporation of Ga causes problems with stability though. Other problems, such as LSGM reactivity with Nickel electrodes have been solved by adding a CeO2 buffer layer between the two materials.
In case of an electrolyte-supported design, the electrolyte has to be 120–150 mm thick. Operation at low temperatures requires a thin electrolyte since the conductivity is proportional to temperature. For operation temperatures between 600–800 °C, the electrolyte layer thickness cannot exceed 20 mm to ensure high enough conductivity.
![]()
Electrolyte fabrication process
The latest production method involves electrochemical vapour deposition used to make tubular cells (at Westinghouse). Doped lanthanum manganite (cathode material) is placed in a low-pressure chamber and zirconium chloride plus yttrium chloride vapour is passed along the outside of the tube, as water vapour is passed on the inside of the tube. A more conventional production method is tape casting:
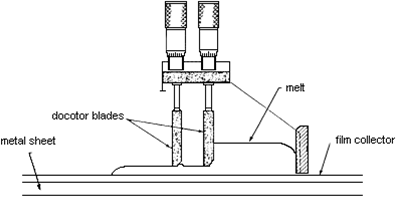
Tape casting
• Electrode materials
This section of the TLP introduces some of the most common materials used as electrodes in SOFCs.
The electrodes have to possess the following properties to ensure a smooth operation of the fuel cell:
- High electrical conductivity
- High catalytic activity
- High surface area
- Compatibility with the electrolyte (and interconnect)
For many years, platinum was the most common and only material that was used as the electrode. The biggest disadvantage of platinum is its cost: it is economically not viable to build fuel cells with platinum electrodes. Hence the pressure to find cheaper electrode materials such as perovskites (e.g. LaCoO3 and LaMnO3) was high. Further development of the perovskites was abandoned because of fast degradation due to their reactivity with YSZ.
The cathode material is very important because the oxidation reaction determines the efficiency of the fuel cell. Since cathodes operate in a highly oxidising environment, it is impossible to use cheap base metals. The best compromise is semiconducting oxides, such as doped lanthanum cobaltites and lanthanum manganites. A new material: La0.8Sr0.2MnO3 (LSM) has the suitable properties: good electronic conductivity and matching heat expansion coefficient. Since the operating temperature of the fuel cells was reduced to below 1000 °C, it is possible to mix LSM with YSZ at 50/50 proportion to form the first surface on the electrolyte. Other materials have been used, such as La0.6Sr0.4Co0.2Fe0.8O3 (LSCF). LSCF has the advantage of lower power losses at lower temperatures and less susceptibility to poisoning by chromium and it is used with ceria based electrolytes.
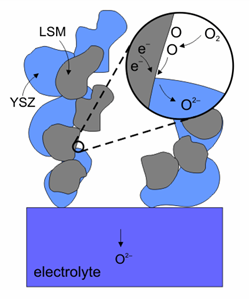
Reduction reaction on the surface of a cathode made of LSM-YSZ.(Image courtesy of Risø National Laboratory)
The loss of cathode performance is mainly due to changes in the microstructure and the phase composition of the material at load conditions. If stainless steel interconnects are used, degradation caused by Cr poisoning occurs, since it evaporates from the steel and condensates preferably on the cathode. In general, the rate at which Cr poisoning occurs decreases with decreasing operating temperature.
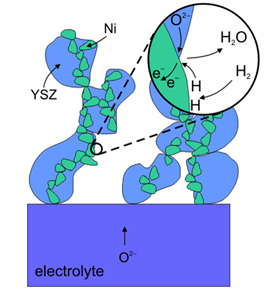
Oxidation reaction on the surface of an anode made of Ni-YSZ (Image courtesy of Risø National Laboratory)
Nickel is used as the anode because it is economical and exhibits high performance, although due to reasons of adherence and different expansion coefficients, it flakes off easily from the electrolyte unless it is mixed with zirconia, creating a cermet. Ni-YSZ anode allows a rapid and clean connection with the fuel and is a good electronic conductor although Ni is susceptible to become coated with a carbon layer when it is reacting with carbon based fuels, which could prevent further reaction. Certain additives to the Ni+YSZ cermet, such as 5% ceria or 1% molybdena inhibit this process. Besides catalysing the oxidation of hydrogen, Ni is also active in reforming of carbon containing fuels. Anodes, completely made of ceramics show good oxidation-reduction cyclability.

Scanning electron micrograph showing a nickel anode
DoITPoMS standard terms of use
The contact sides of the electrolyte with the fuel and the oxidant are coated with the electrode material. To form porous contact layers, partially sintered materials are used and to allow a gradient of properties, such as heat expansion coefficient several layers with different compositions are laid down. Since the gas atoms discharge (or absorb) electrons at the anode (or cathode), a three-phase boundary zone is required:
- Gas phase (high porosity of electrolyte required for better access)
- Electrolyte phase for ion transport
- Metal phase for electron conduction
Hence a volumetric three dimensional region has to be provided for the reaction. The most common methods of applying the electrode layer on the electrolyte are plasma spraying, vapour deposition, solution coating and colloidal ink methods.
• Interconnection
For the interconnection, an inert and impervious material is needed. It should withstand both oxidising and reducing environments. Lanthanum chromite seems to have the necessary properties in systems operating at 1000 °C. Depending on doping, this material matches the thermal expansion coefficient of LSM. For lower temperatures, metallic based alloys can be used. Again, plasma spraying is the most economic method of applying the interconnect layer on the electrode. Although lanthanum provides cell life times of up to 70,000 h, it is not perfectly inert: it expands in the presence of hydrogen, causing cracking, especially at large planar stacks.

Section of SOFC stack with interconnect. From top to bottom: steel, Ni-mesh, cell, contact paste, interconnect steel (Image courtesy of Forschungszentrum Jülich)
Large lanthanum chromite interconnects are made from fine powder, which is prepared as a mixture of the desired components: lanthanum, strontium and chromium nitrate. This mixture is reacted with glycene at high temperatures. This can be compacted to form plates or extruded to make tubes. It is difficult to sinter the powder to full density.
• Thermodynamics
A SOFC is an electrochemical device that converts chemical energy of the fuel and oxidant directly and reversibly into electrical energy. They are not a better or improved heat engine, they are fundamentally different. Hydrogen and oxygen are going to be used to illustrate the thermodynamics of the fuel cell.
![]()
The ideal reversible SOFC – Basic derivation of potential and efficiency
The first and second law of thermodynamics describe the reversible SOFC. The reactants (fuel and air) deliver total enthalpy \(\sum {{n_i}{H_i}} \) and the total enthalpy \(\sum {{n_j}{H_j}} \) leaves the fuel cell, so the change in enthalpy, ΔH = \(\sum {{n_j}{H_j}} \) – \(\sum {{n_i}{H_i}} \). The heat qFC has to be extracted from the fuel cell and the reversible work wFC delivered.
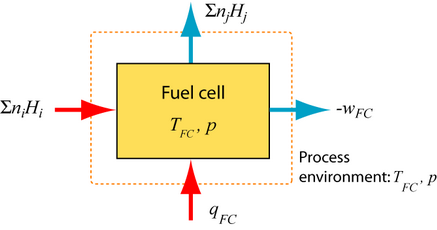
1st Law of thermodynamics: \({q_{FC}} + {w_{FC}} = \Delta H\)
2nd Law of thermodynamics: \(\oint {dS = 0} \)
The reaction entropy has to be compensated by the transport of heat to the environment: \(\Delta S - \) \({{{q_{FC}}} \over {{T_{FC}}}} \)\( = 0\)
The reversible work is from the above equations: \({w_{FC}} = \Delta H - {T_{FC}} \cdot \Delta S\)
The Gibbs enthalpy is equal to the reversible work of the reaction. The reversible efficiency is equal to the ratio of the Gibbs and the reaction enthalpy:
$${\eta _{FC}} = {{\Delta G} \over {\Delta H}} = {{\Delta H - {T_{FC}} \cdot \Delta S} \over {\Delta H}}$$
The fuel cell is an electrical device, for which the processes can be fully described by thermodynamic principles.
Hydrogen is absorbed at the anode, it is ionized and the electrons are conducted away to do useful work. Oxygen atoms that arrive at the cathode are ionized by the electrons coming from the anode. The protons and oxide ions react and form water.
Anode: H2 ↔ 2H+ + 2e– |
This shows that the molar flow of hydrogen is twice the molar flow of oxygen. The electric current is therefore:
$$I = {\dot n_{el}} \cdot \left( { - e} \right) \cdot {N_A} = - 2{\dot n_{{H_2}}} \cdot F$$
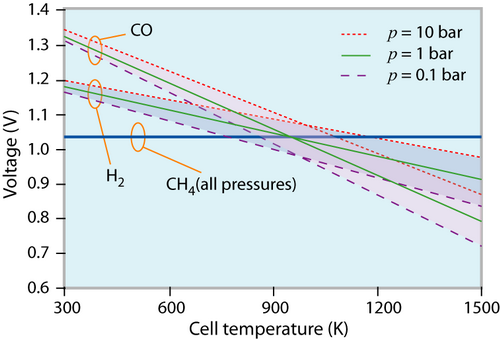
The reversible cell voltage of different fuels at different states (p, T) of the environment
The electric current is a measure of the rate at which fuel is spent. The electric and thermodynamic quantities are matched by considering reversible power:
$$P = V \cdot I = {\dot n_{{H_2}}} \cdot w = {\dot n_{{H_2}}} \cdot \Delta G$$
Hence the reversible voltage:
$$V = {{ - {{\dot n}_{{H_2}}} \cdot \Delta G} \over {{{\dot n}_{el}} \cdot F}} = {{ - \Delta G} \over {{{\dot n}_{el}} \cdot F}}$$
Using the assumption that we have (near) ideal gases, a more accurate equation for the Gibbs energy is:
$$\Delta G(T,p) = \Delta H(T) - T \cdot \Delta S(T,p)$$
where
$$S(T,p) = {S^0} + \int\limits_{{T_0}}^T {{{{C_p}(T)} \over t}dt} - R \cdot \ln ({p \over {{p_0}}})$$
We get for the Gibbs energy:
$$\Delta G(T,p) = \Delta G(T) + T \cdot R \cdot \ln (K)$$
where K is the equilibrium constant.
We get from the above analysis the Nernst potential:
$${V_N} = {{ - \Delta G(T)} \over {{n_{el}} \cdot F}} - {{R \cdot T \cdot \ln (K)} \over {{n_{el}} \cdot F}}$$
![]()
![]() Going further: The chemical thermodynamics of SOFCs.
Going further: The chemical thermodynamics of SOFCs.
![]()
• System and outlook
The operating temperature of an SOFC is relatively high.
A typical SOFC power plant is fuelled with natural gas because of the lack of a hydrogen infrastructure. A plant must have three main components:
1. The preheater raises the temperature of the fuel and air to near the operating temperature. At the same time, the preaheater reforms the gas by steam reforming to hydrogen. Steam reforming constitutes of two steps:
Methane Reforming: CH4 + H2O → CO + 3H2 |
2. The cell stack electrochemically oxidises the hydrogen stream, drawing oxide ions through the electrolyte from the air stream.
Electrochemical reaction: H2 + ½O2 → H2O |
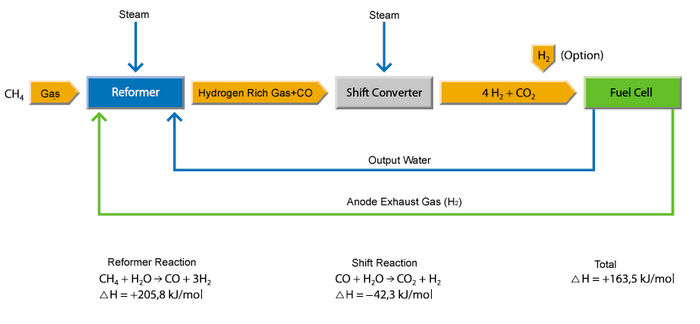
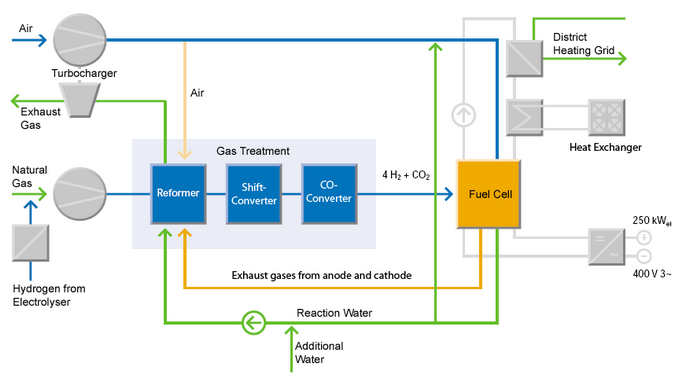
The schematic diagram above depicts a complete, 250 kW fuel cell system (Source: Innovationspark-Brennstoffzelle).
3. The lower cycle utilises the exhaust energy. The exhaust gases are so hot that gas turbines can be driven to generate additional electrical energy and thus increasing the efficiency of the fuel cell system up to 80%.

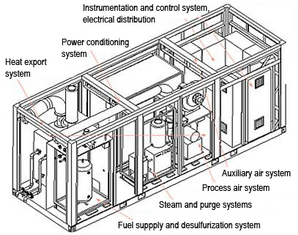
SFC-200, a 125 kW SOFC cogeneration system (Source: Siemens Westinghouse)
The durability of the SOFC is mainly determined by the processes occurring during thermal cycles, oxidation-reduction cycles and the sulphur contamination (even at high temperatures, sulphur is absorbed by the anode).
Fuel
One of the great advantages of the SOFC is that it can use a big range of fuels, depending on the cathode composition. Due to the high operating temperature, internal reforming can take place at the anode, when steam is added to the fuel. The reaction of methane is as follows:
CH4 + H2O → CO + 3H2 |
Both hydrogen and carbon monoxide can react with the oxide ions. A shift reaction also occurs at the anode since the reaction of CO is slow, producing more hydrogen.
CO + H2O → CO2 + H2 |
The disadvantage of using hydrocarbon fuels is the possible formation of coke on the anode:
2CO → CO2 + C |
As mentioned above, impurities, such as sulphur are also damaging to the SOFC. Only desulphurised natural gas can be used as fuel. Other additives (more than 100 different molecules are present in commercial gasoline) can have damaging effects on the nickel anode.
The activity of the nickel anode decreases due to sintering and coke formation when carbon containing fuels are used. The ceramic parts can easily break if vibrational forces are present. This is one reason, why SOFCs are best suited for stationary applications rather than mobile applications.
The ultimate goal is to build a decentralised network of medium sized power generating SOFCs that can supply a small community with electricity with a much higher reliability and minor consequences in case of failure compared to the current system of few but very large power plants.
Molten carbonate fuel cells (MCFCs)
High temperature cells
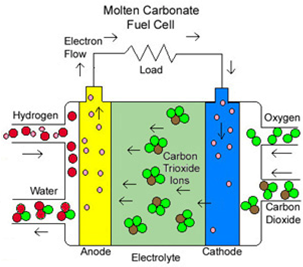
Molten Carbonate Fuel Cells (MCFCs) are another type of high temperature fuel cell. A molten mixture of salts: lithium, sodium, potassium carbonate is used as the electrolyte. These salts melt and conduct carbonate ions (CO32–) from the anode to the cathode when heated to about 600°C. Hydrocarbons have to be used as part of the fuel since the charge carriers in the electrolyte are carbonate ions. Hydrogen is also needed at the anode. It is gained by internal reforming of hydrocarbon based fuels. The electrodes should be resistant to poisoning by carbon. The high exhaust temperature makes cogeneration of electricity with turbines possible; hence the efficiency (60% without and 80% with hybrid technology) is relatively high compared to other fuel cell systems. MCFCs are mainly used for stationary power generation in the 50 kW to 5 MW range. Since it uses a liquid and high temperature electrolyte, it is rather unsuitable for mobile applications. The main problem with MCFC is the slow dissolution of the cathode in the electrolyte. Most of the research is therefore in the area of more durable materials and cathodes.

Molten Carbonate Fuel Cell
DoITPoMS standard terms of use
![]()
Historical summary
Both the solid oxide and the molten carbonate fuel cells are high temperature devices. Their development followed similar lines until the late 1950's. First, E. Baur and H. Preis experimented with solid oxide electrolytes in Switzerland. The technical problems they encountered were again tackled by the Russian scientist O.K. Davtyan without success though. In the late 1950's, Dutch scientists G.H.J. Broers and J.A.A. Ketelaar focused on molten carbonate salts as electrolyte. By 1960, they reported the first MCFC prototype. In the mid-1960's, the US Army’s Mobility Equipment Research and Development Center (MERDC) tested several MCFCs made by Texas Instruments ranging from 100 to 1000 Watts. Ishikawjima Heavy Industries showed in Japan in the early 1990s that a 1000 Watt MCFC power generator can operate for 10000 hours continuously. Other large power plants with outputs of up to 3 megawatts are already planned.

M-C Power's molten carbonate fuel cell power plant in San Diego, California, 1997. Smithsonian Institution, from the Science Service Historical Images Collection, courtesy of National Energy Technology Laboratory.
The MCFC has been under development for 15 years as a stationary electric power plant. Although when most problems with the Solid Oxide Fuel Cell are solved, work on the MCFC might be stopped.
• Electrolyte
In most cases, the electrolyte of the MCFC is made of a lithium-potassium carbonate salt heated to 600-1000°C. At this temperature, the salt is in liquid phase and can conduct ions between the two electrodes. The typical mixture ratio of the electrolyte is 62 m/o Li2CO3 and 38 m/o K2CO3 (62/38 Li/K). This particular mixture of carbonate salts melts at 550°C and when it is mixed with lithium aluminate (LiAlO2 is a ceramic matrix retaining the molten salts, it can be used both as an ion-conducting electrolyte and gasketing for the fuel cell stack. Negative carbonate ions (CO32–) are responsible for conduction. As discussed above, the long term performance is an issue for MCFCs.
The following properties of the electrolyte have to be taken into account:
- Volatility of different alkali metal hydroxides generated in the moist cathode atmosphere
- Solubility of the cathode (NiO)
- Segregation of the electrolytes
- Both oxygen and carbon dioxide solubility in the electrolyte
- Oxygen reduction kinetics
Loss of electrolyte mainly occurs at the cathode via hydrolysis:
MeCO3 + H2O ⇌ 2MeOH + CO2 |
Especially the electrolyte that has been used unaltered for a long time (since Ketelaar and Broers), Li2CO3/K2CO3 (38/62) eutectic, has a relatively high volatility. This causes the fuel cell to dry out.
The partial pressure due to MeOH varies with the square root of water vapour to carbon dioxide vapour pressures:
$$p(M{e_i}OH) = {K_i}(T)\sqrt {{{{p_{{H_2}O}}} \over {{p_{C{O_2}}}}}} $$
Ki(T) is the equilibrium coefficient of the carbonate ion in the melt according to the equilibrium equation:
CO32– + H2O ⇌ CO2 + 2OH– |
The anode off-gas on the other hand can be mixed with air after combustion and reused in the cathode chamber with a sufficiently high air excess. Here oxygen and carbon dioxide are consumed in a ratio of 1:2 (molar) by the cathode process.
The change in composition of the electrolyte due to segregation and the volatility of certain species may result in a change in melting temperature. The electrolyte can solidify, causing the fuel cell to malfunction and sometimes allowing gases to break through. Carbonate ions from the electrolyte are used up in the reactions at the anode, so that we have to compensate for the loss by injecting carbon dioxide at the cathode.
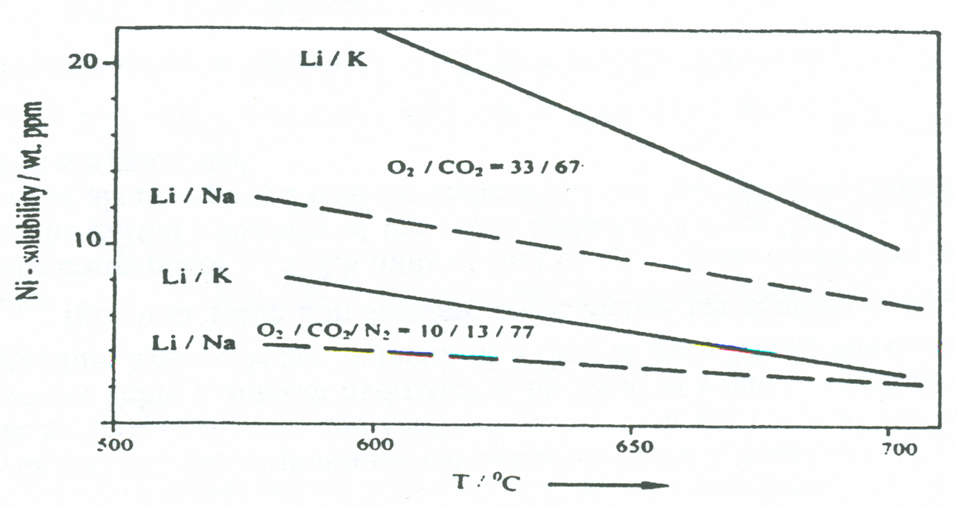
Segregation occurs as the potassium concentration increases near the cathode. This leads to an increased cathode solubility and hence a decline of cell performance.
Recent studies show, that using Na instead of K can decrease the amount of segregation. In a molten binary salt with a common anion, segregation occurs due to the difference in mobilities of the cations. The heavier and bigger potassium and sodium cation is faster lithium in mixtures that have a higher potassium concentration that K2CO3=0.32 (Chemla effect), whereas below this isotachic concentration, lithium is faster.
The partial pressure of carbon dioxide has a much smaller effect on the current voltage curves than the partial pressure of oxygen. Mass transfer limitations are not observed for CO2 but for oxygen at low partial pressures. CO2 transport also hinders the cathode operation much less than oxygen transport since this gas has a much better solubility in carbonate melts than O.
Only the Li2CO3/Na2CO3 eutectic with much lower sodium vapour pressures could assure long term performance of fuel cells. We can conclude that the Li/Na electrolyte is more reliable and safer than Li/K. Since the ionic conductivity of Li/Na carbonate melts is higher than that of Li/K carbonate melts, Li/Na is preferred material as the electrolyte. But since the electrolyte is in the liquid phase, the fuel cell needs a more complex design, compared to other technologies using a solid electrolyte.
• Electrochemistry
External fuel processors are not needed for MCFCs since the fuels can be reformed internally at the high operating temperatures. Internal reforming includes converting methane and steam into a hydrogen rich gas.
CH4 + H2O ⇌ CO + 3H2 |
At the anode, hydrogen reacts with the carbonate ions to produce water, electrons and carbon dioxide.
H2 + CO32– ⇌ H2O + CO2 + 2e– |
The electrons are conducted away by an external circuit to do useful work to the cathode. Oxygen from the air and carbon dioxide from the anode react at the cathode with electrons to form water and carbonate ions.
O2 + CO2 +2e– ⇌ CO32– |
The carbonate ions migrate through the electrolyte to the anode, and complete the electrical circuit. CO32– is used up at the anode; CO2 is needed at the cathode.
• Electrodes
A significant advantage of the MCFC is that non-noble metals can be used as electrodes. At the high operating temperature, a Nickel anode and the Nickel oxide cathode is able to promote the electrochemical reaction. This means lower production costs compared to low temperature fuel cell, where the catalyst electrode is usually made of platinum. The Ni electrodes are less prone to CO poisoning, hence coal based fuel can be used, especially since internal reforming can take place.
 Solubility of electrode in electrolyte
Solubility of electrode in electrolyte
The main problem with the electrodes is their solubility in the electrolyte by Ostwald ripening, which is a dissolution/reprecipitation process. It decreases the internal surface of the porous nickel oxide cathode, causing it to deteriorate. The solubility of nickel oxide (cathode material) is dependant on the cathode potential and temperature. The solubility of Ni and NiO in Li/Na was found to be lower than in Li/K melts.
Although Li/Na melts have been found to have superior performance compared to Li/K melts, the lower oxygen solubility reduces the cathode performance on lean gas with a low oxygen partial pressure (below 0.1 bars).
Proton exchange membrane fuel cells (PEMFCs)
Low temperature cells
The proton exchange membrane (a.k.a. polymer electrolyte membrane) fuel cell uses a polymeric electrolyte. This proton-conducting polymer forms the heart of each cell and electrodes (usually made of porous carbon with catalytic platinum incorporated into them) are bonded to either side of it to form a one-piece membrane-electrode assembly (MEA). A quick overview of some key advantages that make PEMs such a promising technology for the automotive markets:
- Low temperature operation, and hence
- Quick start up
- No corrosive liquids involved
- Will work in any orientation (or zero g for that matter)
- Thin Membrane-electrode assemblies allow compact cells
![]()
Brief history
The PEM fuel cell was developed in the 1960’s in General Electric’s labs. As with so many technologies, the space program and military funded research fast-forwarded it’s development. PEM membranes were first applied to a US Navy project and projects for the US Signal Corps. PEM cells were used in NASA’s Gemini program, which was to serve as a means of testing technology for the Apollo missions. Batteries were not suitable for a journey to the moon because of the extended flight duration. Early PEM systems were, however, unreliable and plagued with leakages and contamination. The systems installed in Gemini spaceships had an operational lifetime of just 500 hrs, although this was considered suitable. Another issue was the water management systems, which are required to keep the membrane hydrated to the correct extent. Apollo designers opted for the more mature technology of AFCs, as did the Space Shuttle designers in the 70's. Recently however, as part of NASA’s program of continuous upgrade on the Shuttles, PEM systems have replaced the aging AFC technology as the primary power source for the Shuttles’ systems. GE decided to abandon their research on PEMFCs in the 70’s, probably due to the cost. At that time, the catalysis required 28 mg of Platinum per cm2 of electrode, compared to the current figure of 0.2 mg cm–2, or less.
Automobiles are arguably one of the most important consumer products on the planet. The finite fuel reserves, which they are chewing through, are not currently a limiting factor, but they will be soon. Much investment has been aimed at developing fuel cell technology for the automotive industry and the electrolyte of choice is the PEM. We’ll look at the problems which automotive companies need to overcome before fuel cell cars hit the street.
However, recent developments in PEMFCs have brought their current densities up to around 1 A cm–2 and cut the platinum requirement to 1% of what used to be needed. The scope of PEMFCs is, arguably, wider than that of any other power supply technology; with the potential to power a range of devices from mobile phones and laptops to busses, boats and houses.
![]()
Construction of the PEM cell
The PEMFC is constructed in layers of bipolar plates, electrodes and membranes:
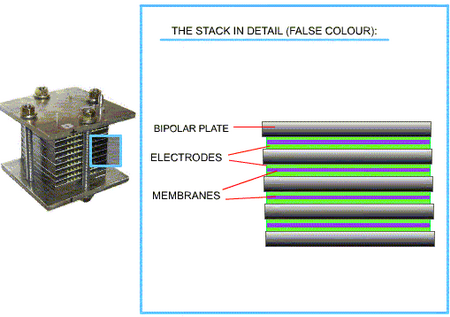
PEMFC components
Each individual cell produces about 0.7 V EMF when operating in air, as calculated by the expressions outlined in the efficiency section. In order to produce a useful voltage, the electrodes of many cells must be linked in series. In addition to connecting the cells, we must ensure that reactant gases can still reach the electrodes and that the resistance of the electrodes has a minimal effect. If, for example, we were to simply wire up the edge of the anode of one cell to the cathode of another, electrons would have to flow across the face of the electrodes. Each cell only produces ~0.7 V, even a small reduction in this isn’t permissible, so cells aren’t normally wired up this way.
A Bipolar Plate is used to interconnect the anode of one cell to the cathode of the next. It must evenly distribute reactant gases over the surface of the anode, and oxygen/air over the cathode. Bipolar plates may also need to carry a cooling fluid, and in addition, need to keep all these gases and cooling fluids separate. Design considerations:
- The electrical contacts should be as large as possible
- The plate should be thin to minimise resistance
- Gas needs to flow easily across the plate
Often these factors are antagonistic to each other, for instance, large contact area would reduce the width of the gas channels. A very simple bipolar plate might look like this:

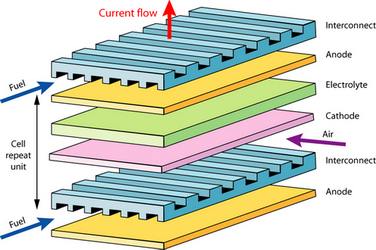
A typical bipolar plate (Left) found in a plate-type PEM assembly (Right)
Reactant gases flow at right angles to each other. In a simple plate design as above, the channels extend right to the edge. The reactant gases would probably be supplied to the system via external manifolding in this case.
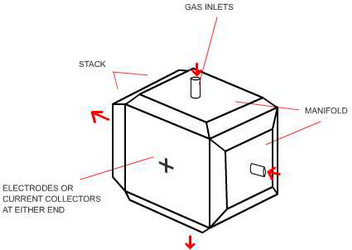
External manifolding
External manifolding is a very simple solution, and therefore carries out the job cheaply, but the technique has two major disadvantages. 1) The gaskets needed to seal the plates don’t form a tight seal where the channels come to the edge of the plate, leading to localised leaks of the reactant gases. 2) Additional channels for cooling fluids are very difficult to incorporate into an externally manifolded system, so all the cooling must be done by the air flowing across the cathode. This means more air than is necessary for the reaction must be pumped through the channels, which in turn means the channels must be wider, that the chance of leaks is increased and that some of the energy produced must be used to power blowers. Whilst simplicity is always a bonus, external manifolding is rarely used in modern systems.

In this image of a Ballard Nexus™ fuel cell system, the fan used to blow air through the stack for cooling is visible on the left of the stack.
DoITPoMS standard terms of use
Most modern bipolar plates make use of internal manifolding. The three examples below show how this might be achieved. In each case, the channels do not run to the edge of the plates so a gasket could be fitted here and a gas-tight seal would be more easily achieved.

Internal manifolding
- The design on the left is a fairly simple parallel channels design; reactant gases would be blown into one end of the channel through one hole, and removed at the other hole. There are many different designs possible, and designers of bipolar plates are yet to reach an agreement on which type is best. In parallel designs, water or gas may build up along one of the channels causing a temporary blockage. In this case the reactants will happily continue to pass through the other channels and not clear the blockage.
- The second design, a serpentine design, guarantees that if reactants are flowing at all, they’re flowing all along the channel and blockages are easily cleared. The problem in this case is that it takes more effort to push reactants through the long, winding path.
- The third design is more of a compromise between the two and is the type of thing often seen in bipolar plate design. The channels are typically about 1 mm in width and depth. The pressure difference between the start and end of a channel must be engineered to overcome the surface tension of water droplets forming on the channel walls in order to clear blockages. Ballard, for example, achieve this pressure difference with rectangular plates in which the gases run across the long axis in a long parallel design.
The material properties of a bipolar plate, as summed up by Ruge and Büchi (2001), must take into account several important factors:
- Electrical conductivity >10 S cm–1
- Heat conductivity of 20 W m–1 K–1 if cooling fluid is integrated, 100 W m–1 K–1 if heat is removed from the edges.
- Gas permeability < 10–7 mbar L s–1 cm–2
- Resistant to corrosion in an environment of acidic electrolyte, hydrogen, oxygen, heat and humidity.
- Reasonably high stiffness E > 25 MPa
- As ever, it should cost as little as possible.
The plates must also be manufactured so that they are:
- Thin for maximum stack volume
- Light for minimum stack mass
- Able to be produced quickly with a short cycle time
These various and difficult specifications which must be met, along with the fact that modern electrodes require very little catalytic platinum, mean that the bipolar plate is the most expensive part of a modern fuel cell.
![]()
![]() Materials for constructing bipolar plates
Materials for constructing bipolar plates
![]()
PEMFCs without bipolar plates
As discussed, bipolar plates may provide excellent contact between cells, but they are expensive and complex. Some manufacturers, often on the smaller industrial scale, choose different techniques to link their cells. Cells could be connected simply edge to edge, reducing the possibility of leakage. One manufacturer (Intelligent Energy) produces cells with stainless steel bases through which hydrogen channels pass. The cathode current collector is a porous metal and these individual cell units are simply stacked with a piece of corrugated stainless steel between them. It’s a simple solution which may gain popularity.
In conclusion, we should note that although a broad range of bipolar plates techniques exist, none of them fully meet the criteria set above. There is lots of development still to be done in this area before we meet a new industry standard.
• Membrane
Dupont’s Nafion™ ion exchange membrane forms the basis of the proton exchange membrane fuel cell. Each company involved in the development of PEMFCs may have their own variation on Nafion, however, they’re all based on the same sulphonated fluoropolymers and Nafion remains something of an industry standard in membranes, to which all others are compared (although it is not always most suitable). Nafion is a polymer based on PTFE (polytetrafluoroethylene).
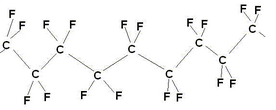
PTFE
Nafion is essentially PTFE containing a fraction of pendant sulphonic acid groups. (Nomenclature: “sulphonic acid group” usually refers to the un-dissociated SO3H group, where as “sulphonate” refers to the ionised SO3– group after the proton has dissociated). The ion containing fraction is normally given in terms of equivalent weight (i.e. number of grams of dry polymer per mole of acidic groups). The useful equivalent weight for Nafion ranges from 800‑1500 g mol–1.
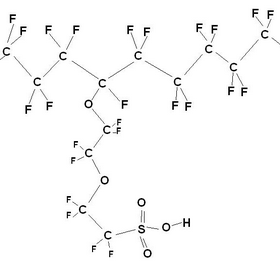
Nafion structure (Left) and a fluoropolymer (Right), made by DOW chemical company, also used in PEMFCs.
The length of and the precise nature of the side chains vary between different brands of polymer. Common to all is the PTFE based fluorocarbon “backbone” of the polymer that has several desirable properties:
- PTFE is hydrophobic - this means the hydrophilic sulphonate groups are effectively repelled by the chains and cluster together.
- PTFE is extremely resilient to chemical attack – the environment within the membrane is hostile and very acidic. Hydrocarbon-based polymers would tend to degrade rapidly.
- PTFE is a thermoplastic with high mechanical strength – meaning very thin membranes can be produced, reducing the thickness of each cell and increasing the power density of the stack.
![]()
Transport through the membrane
The animation below demonstrates schematically the mechanism of proton transport in the proton exchange membrane.
In reality, the protons would be strongly associated with water molecules and transported in the form of H3O+ hydronium ions, or even higher order cations. The Zundel (H5O2+ - basically a protonated water dimer) and the Eigen (H7O3+) cations are thought to be particularly important in transfer of protons from one hydronium to another.
Points to note:
- Sulphonic acids are highly acidic (pKa ~ –6 in Nafion) meaning they have a high tendency to dissociate into anions and protons (the effect of the aliens’ blood in the “Alien” films was produced with chlorosulphonic acid). It is of course, these protons that act as the charge carriers through the membrane.
- In order for the polymer to conduct H+ it must be hydrated to the correct degree, in order to promote dissociation of ionic groups and provide a mechanism for proton transport. Proton conductivity is strongly dependant on the water content of the membrane. The water in the membrane is localised to the hydrophilic groups, where the protons dissociate and are transported in a vehicular manner (by diffusion of hydrated protons) and also structurally (via proton transfer between hydrated clusters).
- Typical PEMs have conductivity in the order of 0.01–0.1 S cm–1 at 80–90 °C, which is a far lower temperature than other solid-state (usually ceramic) electrolytes.
• Electrodes and membrane-electrode assembly
Catalyst
In the first fuel cells, platinum was used in relatively large quantities. This perhaps led to the false belief that most of the cost of a fuel cell is down to the platinum in it. Generally this is not the case. Platinum particles are deposited very finely onto carbon powders so that the platinum is very finely divided with a maximal surface area. With catalysts produced in this way, the raw material platinum cost is just $10 for a 1 kW cell stack.

Catalyst made of carbon powders deposited with platinum particles
DoITPoMS standard terms of use
![]()
Bonding
Before the catalyst layer is applied to the electrolyte, a coating of soluble electrolyte is brushed onto it. This ensures that there is good contact between the platinum and the electrolyte to achieve the important three-phase interaction between gas, catalyst and electrolyte necessary for the reaction to proceed.
The catalyst can be applied to the membrane in one of two ways: Either the catalyst powder can be applied directly to the membrane, by rolling, spraying or printing, and then have the supporting electrode structure (often called the gas-diffusion layer) added afterwards, or the electrodes can be assembled separately and bonded to the membrane in complete form by hot pressing. The catalyst powder is sometimes mixed with PTFE to drive out product water and prevent the electrode becoming water logged. The “gas diffusion layer” is added between the catalyst and the bipolar plate to provide some rigidity to the MEA and to ensure ease of diffusion. This layer is usually composed of carbon cloth or carbon paper 0.2–0.5mm thickness, with more PTFE added to expel water.
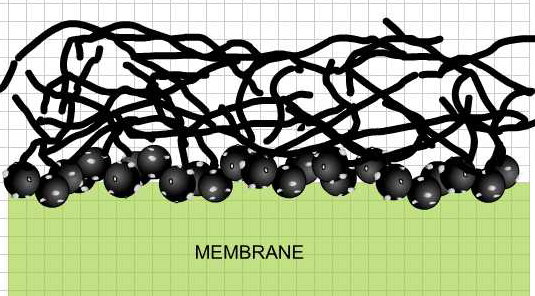
The membrane electrode assembly, once completed.
DoITPoMS standard terms of use
• Efficiency and reaction conditions
The proton exchange membrane is a solid-state electrolyte that functions at around 80 °C. Compared to the 1000 °C at which the solid oxide electrolytes become conductive, this is a low temperature.
![]()
What temperature is preferable?
One of the key banners under which fuel cells are marketed is their efficiency. We must consider how this efficiency comes about and what factors influence it. To do this we must look at the thermodynamics governing the fuel cell.
- Considering the energy of the system - the Gibbs free energy change.
Let's consider the energy of a hydrogen fuel cell system as follows:
INPUTS: |
PROCESS: |
OUTPUT: |
Hydrogen |
FUEL CELL |
Electrical Energy = VIt |
Heat |
||
Oxygen |
Water |
It’s easy to calculate the electrical power and energy output of the system:
Power = VI ; Energy = VIt
The “chemical energies” of inputs and outputs are a little more difficult to define. It is the change in Gibbs free energy that we must consider in this case (or more precisely Gf – the energy of formation - because we use the convention of comparison to pure elements in their standard states), which is the energy available to do external work. In the case of a fuel cell system this external work is pushing electrons through the external circuit, and past whatever impedances we put in their way. Work done by changes in volume and temperature between inputs and outputs is not harnessed by the fuel cell (although this is possible in turbine hybrid systems).
The Gf of both O2 and H2 is zero, a useful result when dealing with a hydrogen oxygen fuel cell. ΔGf refers to the difference in Gibbs free energy of formation between the inputs and the outputs, and is therefore a specific measure of the energy released by the reaction.
ΔGf = Gf of products – Gf of reactants
We usually consider this quantity to be per a mole of chemical. Let us find the chemical energy released during a nominal fuel cell reaction:
H2 + ½O2 → H2O
The Gibbs free energy of a system is defined as:
G = H – TS
Which leads to the change in free energy being expressed as:
(1) \(\Delta {\overline g _f} = \Delta {\overline h _f} - T\Delta \overline s \)
Note that we’ve gone lower-case and added little lines above the letters. This is to signify that we are dealing with molar quantities, so that the units will be Joules per mole or something similar.
The value Δf of is the difference between f of the products and f of the reactants. So for the reaction H2 + ½O2 → H2O, we have:
(2) \( \Delta {\overline h _f} = {({\overline h _f})_{{H_2}O}} - {({\overline h _f})_{{H_2}}} - {1 \over 2}{({\overline h _f})_{{O_2}}}\)![]()
And Δ is the difference between entropy of the products and reactants so that:
(3) \( \Delta \overline s = {(\overline s )_{{H_2}O}} - {(\overline s )_{{H_2}}} - {1 \over 2}{(\overline s )_{{O_2}}}\)![]()
These values of and fvary with temperature and pressure according to the equations given below. A full derivation of these equations is beyond the scope of this TLP but can be found in thermodynamics textbooks. It should be noted that we use 298 K as the standard temperature, which is necessary as an integration limit. The “T” subscript to the enthalpy, , means the enthalpy at temperature T.
(4) $${\overline h _T} = {\overline h _{298}} + \int\limits_{298}^T {{{\overline C }_P}} dT$$
Similarly, the entropy, , at temperature T is given by:
(5) $${\overline s _T} = {\overline s _{298}} + \int\limits_{298}^T {{1 \over T}} {\overline C _P}dT$$
Values for standard enthalpies and entropies are obtainable from tables and some are given below:
|
f (J mol-1) |
(J mol-1 K-1) |
H2O liquid |
-285,838 |
70.05 |
H2O Steam |
-241,827 |
188.83 |
H2 |
Zero (element in standard state) |
130.59 |
O2 |
Zero |
205.14 |
We need to know the molar heat capacity at constant pressure, p. This is not constant with temperature but can be described by empirical equations. Examples below, (units are J g mol-1 K-1):
For H2:
(6) \({({\overline C _P})_{{H_2}}} = 56.505 - 22,222.6{T^{ - 0.75}} + 116,500{T^{ - 1}} - 560,700{T^{ - 1.5}}\)
And for steam:
(7) \({({\overline C _P})_{{H_2}{O_{(g)}}}} = 143.05 - 58.040{T^{0.25}} + 8.2751{T^{0.5}} - 0.036,989T\)
And O2:
(8) \({({\overline C _P})_{{O_2}}} = 37.432 + 2.010,2 \times {10^{ - 5}}{T^{1.5}} - 178,570{T^{ - 1.5}} + 2,368,800{T^{ - 2}}\)
One may now proceed to substitute values of p from equations (6)-(8) into equations (4) and (5) to yield integrals that solve to values of f and for H2O(g), H2 and O2 at any temperature. Substituting these values into equations (2) and (3) gives us values for Δf and Δ, which can in turn be substituted into equation (1) to yield the all-important Δf value.
The table below was calculated using these equations:
Temperature (°C) |
Δf (kJ mol-1) |
25 (liquid) |
-237.2 |
80 (liquid) |
-228.2 |
80 (steam) |
-226.1 |
100 |
-225.2 |
200 |
-220.4 |
400 |
-210.3 |
600 |
-199.6 |
800 |
-188.6 |
1000 |
-177.4 |
which can be handily represented in the following graph:
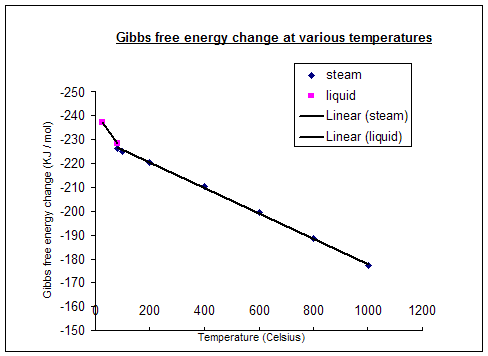
The graph shows us, somewhat obviously, that the energy obtainable from a fuel cell reaction decreases with the temperature at which the reaction is carried out. This however is not the only reason for lack of efficiency at higher temperatures, as we shall see.
![]()
Irreversibilities
This Δf value represents the energy released by the reaction:
H2 + ½O2 → H2O
If there were no losses, if the fuel cell process operated completely reversibly, the fuel cell should be able to convert 100% of this Gibbs free energy into useful electrical energy. However losses, or irreversibilities, creep into every system. For example, some of the energy released in the reaction will inevitably leave the system as heat. Once it has floated away in warmer air, that energy cannot be recovered and turned back into useful electrical energy; so we call it irreversibility rather than a loss.
![]()
 Open circuit voltage
Open circuit voltage
![]()
Back to efficiency
Calculating the efficiency of a fuel cell system is not easy, partly because it is hard to define what the term refers to in this situation. It would help to look at a situation where efficiency is a little more obvious. The efficiency limit of a heat engine (such as a gas or steam turbine or an internal combustion engine) is defined as:
$${\rm{Carnot\;\; Limit}} = {{{T_1} - {T_2}} \over {{T_1}}}$$
T1 stands for the maximum temperature of the engine and T2 represents the temperature of the exhaust, all in Kelvin. The limit stems from the fact that there is always going to be some energy, proportional to the T2, which is “lost”.
We know that fuel cell systems are not seconded to this limit; so how do we give a measure of their efficiency? We have already seen that it is the Gibbs free energy that is converted into electrical energy. If not for irreversibilities, all of this could be converted to electrical energy giving a 100% maximum efficiency. We could therefore define the efficiency of a fuel cell system as:
$${{{\rm{Electrical\; energy \;output}}} \over {{\rm{Gibbs\; free\; energy\; change}}}}$$
When this is the case however, no matter what the reaction conditions are, the efficiency limit is 100% and therefore the figure isn’t really much use to anybody.
A common measure of the energy contained in a fuel is its calorific value. This is a measure of the heat that would be produced by burning the fuel. A more precise measurement is the change in enthalpy of formation, Δf and as with the Gibbs energy, the convention is that a negative value translates to more energy released during reaction. Using this value we can obtain a more useful efficiency value for a fuel cell:
$${{{\rm{Electrical\; energy \;output \;per \;mole \;of \;fuel}}} \over {\Delta {{\bar h}_f}}}$$
Recall however that the Δf of steam is different to that of liquid water, hence there are two possible efficiency values for a given process depending on the state of the output. See table below listing the Δf values of the reaction H2 + ½O2 → H2O, depending on the form of the product.
H2O liquid |
-285,838 |
H2O Steam |
-241,827 |
Papers quoting an efficiency value will usually say whether it refers to the higher heating value, the HHV (in which steam is the product); or the lower heating value, the LHV.
We can express maximum possible efficiency as:
$${{\Delta {{\overline g }_f}} \over {\Delta \overline {{h_f}} }} \times 100\% $$
Which is often termed the “thermodynamic efficiency” of the fuel cell. We can use this equation along with equation 9 to come up with various efficiency limits and maximum reversible EMF values. These are listed in the table below, which is an extension of the earlier table:
Temperature (°C) |
Δf(kJ mol-1) |
Max EMF (V) |
Efficiency Limit |
25 (liquid) |
-237.2 |
1.23 |
83% |
80 (liquid) |
-228.2 |
1.18 |
80% |
100 |
-225.2 |
1.17 |
79% |
200 |
-220.4 |
1.14 |
77% |
400 |
-210.3 |
1.09 |
74% |
600 |
-199.6 |
1.04 |
70% |
800 |
-188.6 |
0.98 |
66% |
1000 |
-177.4 |
0.92 |
62% |
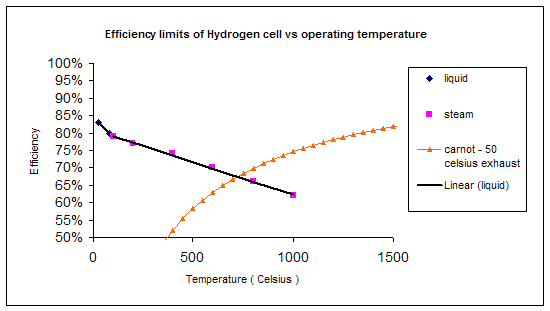
![]()
Are higher temperatures better?
Points to note about the graph above:
- The graph above is quite specific to the hydrogen fuel cell. If we were to look at the cell fuelled by CO:
CO + ½O2 → CO2
We’d see the Δf becomes less negative even faster with increasing temperature so that the efficiency limit of 82% at 100 °C falls to 52% at 1000 °C. On the other hand, the Δf of the methane fuelled reaction:
CH4 + 2O2 → CO2+ 2H2O
Hardly changes with temperature so the efficiency limit stays consistent. We must therefore remember that the temperature dependency of efficiency is characteristic to a reaction.
- It can be seen that fuel cells do not always have a higher efficiency limit than fuel cells.
Since the efficiency limit of the H2 fuelled cell reduces with operational temperature, one might be tempted to conclude that hydrogen fuel cells should be run at the lowest possible temperature. There are several reasons why this is not the case:
- In higher temperature systems, the heat produced can be more useful. Turbine hybrid systems can be used to utilise the energy of the exhaust gases. This isn’t as easy if the fuel cell is run at low temperatures.
- The voltage losses (discussed later in this section) of the cell, the irreversibilities which are an inevitable part of the process, are generally more significant at higher temperature.
![]()
 Fuel utilisation and reaction optimisation
Fuel utilisation and reaction optimisation
![]()
In conclusion, the factors determining the efficiency of the system are manifold and various. We can estimate the efficiency obtained by simply measuring the open circuit voltage of the fuel cell Vc and we can make sense of this by looking at the reaction and how the Gibbs free energy is transferred between reactant and product species.
Fuelling requirements
Cell Type
|
Fuelling requirements |
Solution |
||||||||||
AFC |
Alkaline fuel cells, using KOH as the electrolyte, require pure H2 and O2 as their fuel. This is because even the small amounts of CO2 in the air (about 300 ppm) are enough to prevent the cell from functioning properly. This is because CO2 reacts with the KOH as follows: 2KOH + CO2 → K2CO3 + H2O The presence of potassium carbonate in the electrolyte may reduce cell activity by:
|
Use of Pure Oxygen at the cathodes is necessary. This can be achieved by:
|
||||||||||
Species: |
H2 |
CO |
CH4 |
CO2 and H2O |
S (e.g. H2S and COS) |
|||||||
Effect: |
Fuel |
Poison |
Diluent |
Poison |
Unknown |
|||||||
PAFC |
The phosphoric acid (H3PO4) systems are almost always fuelled by a hydrocarbon, which must undergo some sort of fuel processing (add link) to release the H2 gas that reacts at the anodes. The PAFC systems can tolerate CO2 and un-reacted hydrocarbons (e.g. methane). These act as diluents to the fuel and their concentrations should be minimised. CO gas however will poison the Pt catalysts at concentrations from 0.5% |
|
||||||||||
Species: |
H2 |
CO |
CH4 |
CO2/H2O |
S etc |
|||||||
Effect: |
Fuel |
Poison (>0.5%) |
Diluent |
Diluent |
Poison (>50 ppm) |
|||||||
MCFC |
CH4 can either be a diluent or it may be internally reformed (see SOFCs). Very low sulphur tolerance in the MCFC due to poisoning, especially in the catalysts that aid fuel reforming. The reactions of the MCFC requires CO2 to be present in the fuel: Recall that CO32– ions are transported through the electrolyte from cathode to anode (see section on high temperature fuel cells). This requirement for CO2 contrasts with the AFC where it must be excluded. The CO2 is usually recycled externally by passing exhaust gases through a combustor to convert unused fuel into water and CO2, which can be fed back to the cathode inlet. This also serves to preheat the reactant air. |
|
||||||||||
Species: |
H2 |
CO |
CH4 |
CO2/H2O |
S etc |
|||||||
Effect: |
Fuel |
Fuel (via shift reaction) |
Can be internally reformed |
Diluent |
Poison (>0.5 ppm) |
|||||||
SOFC |
SOFCs (and MCFCs) run at high enough temperatures to internally reform CO and hydrocarbons (e.g. petrol or methane) via reaction with H2O, producing CO2 and H2 via “shift” (or oxygenolysis) reactions:
|
|
||||||||||
Species: |
H2 |
CO |
CH4 |
CO2/H2O |
S etc |
|||||||
Effect: |
Fuel |
Fuel (via shift reaction) |
Can be internally reformed |
Diluent |
Poison (>1.0 ppm) |
|||||||
PEMFC |
PEM Cells generally use pure Hydrogen as the fuel, especially in portable applications where complicated reforming apparatus would be impractical. CO poisons PEM systems very easily because they rely on platinum catalysts. CO has a high affinity for Pt and occupies catalytic sites, preventing hydrogen fuel from preaching them. The processing equipment needed to reduce CO partial pressures to less than 10 ppm adds considerably to the cost of the system.
|
|
||||||||||
Species: |
H2 |
CO |
CH4 |
CO2/H2O |
S etc |
|||||||
Effect: |
Fuel |
Poison (>10 ppm) |
Diluent |
Diluent |
Unknown |
|||||||
Case study: Fuelling practicalities
Supplying the cell’s anodes with a constant and consistent supply of hydrogen is no small task. The following diagram shows some ways this can be achieved:
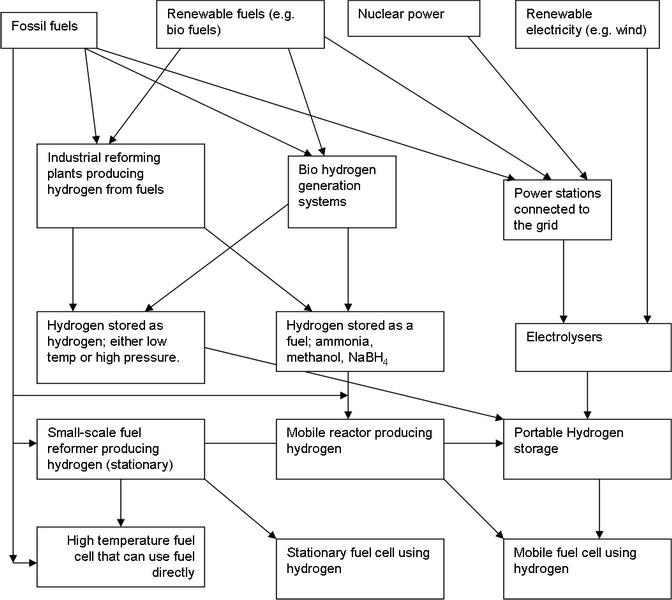
This diagram should be considered it in terms of three levels; where we obtain the energy, how it is used to make hydrogen, and how that hydrogen is stored and used at the cell.
Crude oil derived fuels still account for more than half of the world’s total energy supply (petrol, diesel, aviation fuel, kerosene). These consist of simple and aromatic hydrocarbons of varying length. Add to this the consumption of coal and natural gases and the fossil fuel contribution to global energy supply goes well above 80%. Fossil fuels can either be utilised directly in some high temperature fuel cells, or reformed to hydrogen (see notes on reformers), or used in conventional power plants to produce electricity, which could then power electrolysers.
Renewable fuels are useful bio-matters, such as wood or plants, and renewable gas sources such as the methane produced as waste in landfill sites decomposes. These can again be used to make hydrogen by reforming, bio-generation or by conventional power plants and electrolysers. Nuclear power can power electrolysers to make hydrogen indirectly. The animation below summarises the above:
![]()
Fuel storage
Once we have the hydrogen, there are several ways in which it can be stored:
- Compression in gas cylinders
- Cryogenic liquid
- A metal absorber as a metal hydride
- Potentially in carbon nano-fibres (still under development)
- Glass micro-spheres
The specific energy of pure hydrogen (the energy per kilo) is higher than any other fuel at about 120 MJ kg-1. However, its energy density (energy per m3) is very low.
Form of storage |
Energy density by weight |
Energy density by volume |
Gas (20 MPa) |
33.3 |
0.53 |
Gas (24.8 MPa) |
33.3 |
0.64 |
Gas (30 MPa) |
33.3 |
0.75 |
Cryogenic liquid (-253 °C) |
33.3 |
2.36 |
Metal hydride |
0.58 |
3.18 |
It’s difficult to get a large mass of hydrogen into a small volume. Whilst fossil fuels can be processed to provide an on-demand supply of hydrogen, or even utilised directly by some cells, there are many applications for which a pure hydrogen supply is the only viable solution. These applications might include anywhere where there is limited space for reforming equipment or where it would be too costly, where emissions must be tightly controlled perhaps or where adding the additional fuel processing equipment would unacceptably reduce the efficiency of the system. Electrical energy output from wind turbines and hydroelectric generators might also be stored as hydrogen.
The safe storage of pure hydrogen presents a tempting challenge to engineers and material scientists. Either very high pressure must be used to squeeze the required mass into a required volume, or very low temperatures used to liquefy it. Hydrogen however, does not liquefy above 22K and even in its liquid phase has rather a low density of 71 kg m-3.
![]()
Ways of storing pure H2
Method: |
Pros: |
Cons: |
High-pressure storage of gas. Hydrogen gas can be stored at pressures of up to 30 MPa (300 atm). Composite tanks can be used with aluminium liners and a Kevlar-epoxy shell. |
|
|
Liquid hydrogen (LH2) stored at 22 K in thermally insulated tanks, usually like large vacuum flasks. State of the art tanks cool the 22 K LH2 with liquid air at 78 K. |
|
|
Metal hydrides |
|
|
Glass micro-spheres can be encouraged to absorb H2 gas at higher temperature, then retain it at lower temperatures before releasing it again when the temperature is raised. A technology yet to be proven.
|
|
|
Carbon nano-fibres
Structure of carbon nano-fibres |
|
|
![]()
![]()
Summary
Problems such as CO2 emissions and the sustainability of our current energy supplies are going to result in the western world adopting lasting changes to the way we harness energy. It is likely that fuel cell technology has an important part to play in this future.
This TLP should have taught the following:
- The principles, construction and thermodynamics of a fuel cell
- Differences between types of fuel cell – high temperature, low temperature, the key components of each.
- How the technology can be applied and possible future applications
- The complications involved in the fuel cell system as a whole
- The basis of a future hydrogen economy
- Problems associated with storing hydrogen
It is important to remember that the sums spent on developing fuel cells thus far have been very large indeed but, as of yet, returns are sparse. Few people will encounter fuel cells as part of their every day lives, but perhaps this is set to change in near future.
Questions
Quick questions
You should be able to answer these questions without too much difficulty after studying this TLP. If not, then you should go through it again!
-
For each type of fuel cell below, what are the charge carrying species (electrolyte type)?
(a) Polymeric exchange membrane
(b) Immobilised alkaline solution
(c) Phosphoric acid
(d) Molten carbonate
(e) Ceramic solid oxide -
Which cells are able to internally reform?
-
The efficiency limit of H2 cells reduces as operating temperature is increased. Why are high efficiency systems often run at very high temperatures?
-
Which of the following statements are TRUE about the development of fuel cells?
(a) Fuel cells have been around since the 19th century.
(b) A fuel cell tractor was built in 1959.
(c) PEM fuel cells are so expensive because of the platinum needed as a catalyst.
(d) The first fuel cells were developed to run on hydrogen.
(e) Fuel cell cars are at least a decade away. -
Give two reasons why we don’t all use fuel cells in our cars already?
-
Why is nickel used as the anode in SOFCs? How is it treated in order to aid bonding to YSZ?
Deeper questions
The following questions require some thought and reaching the answer may require you to think beyond the contents of this TLP.
-
Give as many ways as you can think of to provide a mobile fuel cell with pure hydrogen.
Going further
Books:
1. J. Larminie and A. Dicks, Fuel Cell Systems Explained, 2nd edition, John Wiley and Sons Ltd (2003).
2. M.H. Westbrook, The Electric Car: Development and Future of Battery, Hybrid and Fuel-Cell Cars, London: Institution of Electrical Engineers; Society of Automotive Engineers (2001).
3. High-temperature Solid Oxide Fuel Cells: Fundamentals, Design and Applications by S.C. Singhal and K. Kendall (Eds.), Publisher: Elsevier Science (2004).
Short video showing a demonstration fuel cell car
Building a simple fuel cell – just like Billy Grove did
Collect the necessary components:
This is the most challenging part of the project, due to the difficulty many students will have in procuring the two lengths of platinum (Pt) wire required. Persist.
- Two short lengths of platinum wire – 2 cm a piece is sufficient
- A beaker
- Weak NaCl solution (table salt and tap water will suffice)
- Crocodile clips ×2
- Wires ×2
- Voltmeter
- DC power source, e.g. 6-volt battery
Step by step:
- Fill beaker with salt solution
- Clamp the ends of the Pt wires in the crocodile clips
- Place the Pt wires in the solution in such a way that they will not move
and so that only the Pt is in contact with the water. Plasticine (or Blu-Tac)
would be helpful at this point. If the crocodile clips are in contact with
the solution they will corrode quickly and taint the water.
- Verify that the voltage across the two electrodes is zero (two wires made
of the same metal have no galvanic difference between them and hence no voltage
will be seen).
- Connect each Pt wire to one of the battery’s terminals and watch the
gas bubbles from the electrodes.
- Verify that the voltage across the electrodes is now equal to that of the
battery, i.e. 6 V.
- Disconnect the battery and be careful not to knock the beaker.
- Verify that a voltage remains across the two electrodes.
This remaining voltage is due to bubbles of chlorine gas adhering to the cathode and to bubbles of hydrogen gas adhering to the anode. HCl is produced as the two atoms combine, via H+ ions travelling through the solution from anode to cathode, to produce HCl.
![]()
Things to consider:
An ammeter will confirm that we only obtain a tiny current in the above experiment (although the voltage remains set to the value we can calculate using the Nernst equation). Factors limiting the current in this case are:
- the small surface area of the electrode - small amount of gas
- wide spacing of the electrodes and electrolyte's ionic resistance.
In production cells, the electrodes are made larger and flat so as to maximise contact area, and the thickness of the electrolyte is kept to a minimum so as to reduce resistance.
Other types of fuel cells?
A fuel cell is defined as an electrochemical device that converts chemical energy to electrical energy (and heat) as long as reactants are supplied to its electrodes. In contrast to batteries, this implies that neither the electrodes or the electrolyte are used up by the operation of the cell, hence the fuel cell should keep running (wear and tear excepted) as long as fuel is supplied. These examples of “fuel cells” don’t all fulfil this criterion but are commonly mislabelled anyway.
- A “biological fuel cell” is still at the very early stages of development but shows promise in the long term. They would use an organic fuel such as natural gas or an alcohol. The key feature of this type of cell is that they would use enzymes rather than chemical catalysts (e.g. Pt) to facilitate the electrode reactions. This idea seeks to replicate nature, but it’s a long way from practical application.
- Metal/air cells such as the zinc air battery use an alkaline salt solution to act as an electrolyte with OH– as the charge carrier. At the anode, zinc is slowly corroded away to zinc oxide in the solution. The cell could be “refuelled” by adding more zinc to the electrode, but the fact that electrodes are consumed means that this is a battery rather than a fuel cell. Such cells do have high energy density and are commonly used for long life, low power applications. They are often called fuel cells because the cathodic reaction is identical to that in the fuel cell.
 Wind turbine
Wind turbine
Britain is the windiest country in Europe, so why are we not using wind turbines to supply a larger portion of our energy needs? The problem is that wind is a gusty phenomenon that is intrinsically inconsistent. Energy storage on a large scale must be a realisable technology before such energy sources can be utilised. Redox fuel cells are being developed as a means of storing energy.

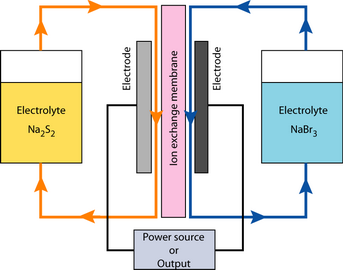
A Regenesys plant which was under construction near Cambridge (Left) and the principle behind a Redox fuel cell (Right).
Two different solutions are contained in two tanks. When energy is required, a solution of Na2S2 is fed to the anode, and NaBr3 to the cathode. The anodic reaction is:
2Na2S2 → Na2S4 + 2Na+ + 2e– |
The electrons flow around the external circuit so that at the positive electrode, or more precisely the cathode (remember, the definition is that the anode is the site of oxidation), we see:
NaBr3 + 2Na+ + 2e–→ 3NaBr |
As energy is drawn from the system, the sodium sulphide becomes sodium polysulphide and the tribromide becomes sodium bromide. This reaction is reversed when current is supplied to the cells. The system is called a fuel cell because the electrodes are just a surface for the reaction, and are not consumed by it. They are also fed and energy containing liquid. The electrolytes however are not really fuels and they are changed during the process. This system should probably be called a strange-battery.
- Proton Exchange Ceramic (PEM) fuel cells do exactly what they say on the tin. They will utilise fossil fuels directly, at around 700 °C, reducing them at the anode and conducting protons across a ceramic electrolyte. They are at the very early stages of development, but potentially have a great advantage over the low temperature PEM cells in that high temperature exhaust gases can be used in a turbine hybrid system to generate more electricity and push the system’s efficiency up to around 80%.
The chemical thermodynamics of SOFCs
The reactant properties and fuel cell condition determines the electrical potential difference between the anode and the cathode electrode. The following analysis assumes quasi-static equilibrium and a steady flow of gas and ions.
At the cathode-electrolyte interface, the following half reaction occurs:
(1) ½O2 + 2e– ↔ O2–
In equilibrium the sum of the chemical potentials is zero:
(2) \({\textstyle{1 \over 2}}{\mu _{{O_2}}} + 2({\mu _{{e^ - }}} - F \cdot {\Phi _C}) = ({\mu _{{O^{2 - }}}} - 2F \cdot {\Phi _E})\)
Rearranging equation (2) gives:
(3) \({\Phi _C} - {\Phi _E} = \)\({\textstyle{1 \over {2F}}}\)\(({\textstyle{1 \over 2}}{\mu _{{O_2}}} + 2{\mu _{{e^ - }}} - {\mu _{{O^{2 - }}}})\)
At the anode-electrolyte interface, the following half reaction occurs:
(4) H2 + O2– ↔ H2O + 2e–
In equilibrium the sum of the chemical potentials is zero:
(5) \({\mu _{{H_2}}} + ({\mu _{{O^{2 - }}}} - 2F \cdot {\Phi _E}) = {\mu _{{H_2}O}} + 2({\mu _{{e^ - }}} - F \cdot {\Phi _A})\)
Rearranging equation (5) gives:
(6) \({\Phi _A} - {\Phi _E} = \)\({\textstyle{1 \over {2F}}}\)\(({\mu _{{H_2}O}} + 2{\mu _{{e^ - }}} - {\mu _{{H_2}}} - {\mu _{{O^{2 - }}}})\)
Hence we can calculate the electric potential difference between the anode and the cathode:
(7) \({\Phi _C} - {\Phi _A} = \)\({\textstyle{1 \over {2F}}}\)\(({\mu _{{H_2}}} + {\textstyle{1 \over 2}}{\mu _{{O_2}}} + {\mu _{{H_2}O}})\)
Assuming that the gases behave like ideal gases, we can write for the chemical potential:
(8) \(\mu (T,p) = {\mu ^o}(T) + RT \cdot \ln ({\textstyle{p \over {{p_o}}}}) + RT \cdot \ln ({x_i})\)
xi is the mole fraction of component i, mo(T) is the chemical potential per mole of an ideal gas at po = 1 bar.
Substituting (8) in (7), we can write:
(9) \({\Phi _C} - {\Phi _A} = {\textstyle{1 \over {2F}}}({\mu _{{H_2}}}^o + {\textstyle{1 \over 2}}{\mu _{{O_2}}}^o - {\mu _{{H_2}O}}^o) + {\textstyle{{RT} \over {2F}}} \cdot \ln ({\textstyle{{{x_{{H_2}}}\sqrt {{x_{{O_2}}}} } \over {{x_{{H_2}O}}}}}) + {\textstyle{{RT} \over {4F}}} \cdot \ln ({\textstyle{p \over {{p_0}}}})\)
Materials for constructing bipolar plates
Materials used and manufacturing techniques vary a lot between producers. One thing many manufacturers have in common is that the plates are often produced in two halves and stuck together afterwards. This makes it easier to have cooling fluid channels running through the body of the plates as instead of drilling holes through them, one can mill away the surface of two half plates and then combine them.
Some manufacturing techniques and materials (the two are usually intrinsically linked) are outlined below:
![]()
Graphite based
- Graphite sheet machined with channels
Advantages:
- Easily machined by automated processes
- Light weight material
- Good conductive material
Disadvantages:
- Graphite is porous and therefore the plates need to be relatively thick.
- Whilst the machining of channels is a fairly easy process, it is one that takes a long time – considerably increasing the production cycle time.
- Graphite is brittle meaning that the plates must be handled carefully – making assembly difficult.
- Injection moulded graphite filled polymer resins
Advantages:
- Very cheap technique
- Short production cycle
Disadvantages:
- The polymers aren’t generally conductive enough to be useful, however developers working on these techniques recently, with epoxy resins and course graphite, claim 75% graphite content and through plane conductivity of 20 S cm-1. This technique could become useful in the future.
- Compression moulded graphite particles in a thermoplastic polymer:
This technique involves a mixture of graphite and thermoplastic granules in a mould, heated above the glass transition temperature (Tg) of the polymer under pressure until the materials mix together and flow into the mould.
Advantages:
- Can use a higher proportion of carbon particles than in the injection moulded method meaning conductivity is greater.
- The technique and the machinery involved are relatively simple.
Disadvantages:
- Very slow production cycle (~15 min) as the mould must be cooled before each half plate can be removed.
- Carbon-carbon composites:
There are a couple of ways of using carbon-carbon composites in bipolar plates. The complex channels of the plate are formed by moulding a carbon composite in one of the two ways outlined below, but this alone doesn’t produce a plate that is strong enough, flat enough or impermeable enough to meet our specifications (basically too flimsy). A layer of solid carbon is applied to the back of this plate to improve properties.
One possible process involves the graphitisation of a carbon powder in a mould by heating it to 2500 ºC. This is expensive and requires a very precise control of temperature. It does have the advantage of relative simplicity of concept. The alternate method used is to mould the channels from a suspension of short carbon fibres in a phenol resin, which is then cured at 150 ºC for a few minutes to give a very high conductivity (>200 S cm-1) but high porosity plate. The back of this can then be made hermetic by depositing a layer of solid carbon via chemical vapour deposition.
Advantages:
- High stiffness
- High conductivity
- Low permeability
- Can be done quickly
Disadvantages:
- Quite expensive materials involved
![]()
Metal based
Metals have several advantages over carbon based plates:
- Much higher conductivity of heat and electricity
- Very easy machining (e.g. stamping)
- Non porous (can be made thin)
- High modulus
- Can be low cost
However, the major disadvantage is their susceptibility to corrosion. The fuel cell environment is hostile. To protect a metal plate from corrosion requires some sort of treatment that would negate one or more of the advantages of using metal plates in the first place; for example, stainless steel plates could be used, which would be resistant to corrosion but which are expensive to produce and difficult to machine. Coatings are a practical possibility, but add to the cost again.
The use of metals in bipolar plates does however make way for some novel designs. The image below is of titanium foamed with argon. Titanium is a poor conductor compared to other metals, but it is still 30 times more conductive than graphite. Metallic foams allow great electrical contact with the whole surface of the cell, and at the same time allow gases to get to the whole surface. The foam does however have a tendency to clog with product water. One approach to this problem involves impregnating areas of the foam with epoxy or even simply crushing areas of it, so as to create channels of porosity in a similar way to the channels cut in carbon plates.
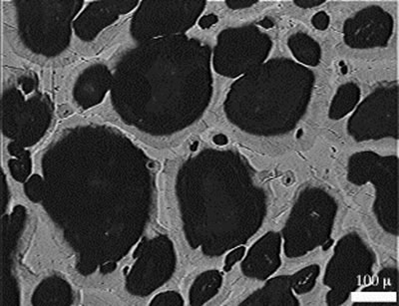
Titanium foamed with argon (Source: North Western Edu)
A major selling point of this metal foam approach to the bipolar plate is the simplicity of joining the components. The foam can be produced in blocks and then sliced like cheese. Add a thin sheet of impermeable metal between two slices of foam, surround it all with a gas-tight seal and add the connecting tubes and you have an effective bipolar plate. Titanium is also an easily protected material by means of nitriding the surface.
Fuel utilisation and reaction optimisation
In practice, not all the fuel supplied to the anode can be reacted; some must pass through as it is. If all the fuel supplied to the electrodes was oxidised, we’d see areas of the anode at which there were lower fuel concentrations at any given time, so as a whole the fuel cell wouldn’t be operating to its full potential. Instead it’s better to have some of the fuel pass through un-reacted. We therefore need to consider the factor of fuel utilisation in our efficiency calculations. The utilisation co-efficient μf is given as:
$${\mu _f} = {{{\rm{Mass\; reacted}}} \over {{\rm{Mass\; input}}}} \approx {\rm{ 95\% }}$$
Typically, only 5% of the fuel supplied should pass through un-reacted. This of course can be re-circulated to the cell. We can put this value of μf into the calculations like this:
Recall that EMF of the hydrogen cell is given by:
$$E = {{ - \Delta {{\overline h }_f}} \over {2F}} = 1.25{\rm{ V}}$$for the lower heating value (steam product)
Using the cell voltage Vc it is possible to estimate the efficiency η:
$$\eta = {{{V_c}} \over {1.25}} \times 100\% $$
and then we take account of the fuel utilisation co-efficient like this:
$$\eta = {\mu _f}\left( {{{{V_c}} \over {1.25}}} \right) \times 100\% $$
Hence we can estimate the efficiency of a cell by measuring its voltage and knowing a little about how it works.
![]()
Voltage losses
We’ve seen the limits of efficiency, but due to voltage losses, fuel cells will never operate at these limits. There are 4 main losses to be considered:
- Fuel crossover – The electrolyte is never a perfectly impermeable material with respect to the fuel gas and also with respect to electron conductivity. It should be noted that an electron pair crossing the electrolyte from the cathode to anode is essentially the same as a molecule of fuel crossing the other way. Both events serve to waste just a little fuel. Fuel crossover is summarised in the animation below:
- Ohmic losses – These are simply losses due the resistance of the system. These become significant in higher temperature cells such as SOFCs and much effort goes into minimising loss of this kind.
- Mass transfer losses – This refers to the fact that concentration of reactants at the electrodes affects voltage, as we have seen using the Nernst equations. If the reactant concentrations fall in some area of the electrode for some reason, then the cell does not work to its maximum efficiency. The extent of the concentration changes around the electrodes depends on the current drawn and on how well the reactant gases are circulated.
- Activation losses – This refers to the slowness of the reaction due to the activation over-potential needed to make it work. Activation over-potential follows a Tafel equation like this:
$$\Delta {V_{act}} = A\ln \left( {{i \over {{i_0}}}} \right)$$
Where i is the current density and i0 is the exchange current density at which we see no net reaction.
Each fuel cell type will be more susceptible to a different kind of voltage loss. These are discussed in more detail in their respective sections.
![]()
Optimum pressure
In equations (10) and (11), we introduced the concept of activity as being an important factor determining the EMF of a cell. Activity has a large dependence on both ambient pressure and the partial pressure of the reactant gas. Higher pressure leads to higher power but pressurised systems are heavier and require more energy to run. Therefore determining the optimum pressure for a given application and system is a difficult task, and it’s often solved by a computer program.
Note: If dealing with PEMFCs, a minimum of 2 bar at 80 °C must be maintained to achieve the humidity required for the membrane to conduct.
Optimum humidity
A PEM requires a certain degree of humidity to function, this is often achieved by complicated water management equipment and control systems. The optimum humidity is once more a difficult parameter to calculate. Too dry and the membrane won’t conduct H+, where as too humid and product water won’t dissipate, clogging the electrodes and preventing gases from reaching the catalysts.
Open circuit voltage
Now that we know how much energy can be released by the reaction at a given temperature, we can find the open circuit voltage of the cell:
For every mole of hydrogen used by the cell, 2 moles of electrons flow from anode to cathode via the external circuit. The charge that flows per a mole of hydrogen consumed / water produced is therefore:
–2NAe = –2F
where NA is the Avogadro’s number, –e is the charge on an electron and F is Faraday’s constant; the charge on a mole of electrons. If E is the voltage of the cell, then the energy required to move this charge around a circuit is:
Electrical work done = charge × voltage = –2FE joules
If the system were totally reversible (i.e. no losses), this work would be equal to \(\Delta {\overline g _f}\) such that:
$$\Delta {\overline g _f} = - 2F \cdot E$$
Which re-arranges to:
$$E = {{ - \Delta {{\overline g }_f}} \over {2F}}$$
And which generalises to:
(9) \(E = \){{ - \Delta {{\overline g }_f}} \over {zF}}\)
where z represents the number of electrons transferred for each mole of fuel. And hence we have an expression that tells us the EMF of the cell (which is the open circuit voltage with no losses). This value assumes no irreversibilities (i.e. 100% efficiency) and that the cell is fuelled by hydrogen and oxygen at standard pressure of 1 atm (0.1 MPa). Using oxygen from the air at the cathode is equivalent to supplying oxygen at a lower pressure. We can take pressure into account using the Nernst equation.
We’ve already noted that temperature has an influence on the important \(\Delta {\overline g _f}\) value.
Pressure variation has a more complex, but just as significant effect. Considering a general reaction such that:
$$jJ + kK \to mM$$
Where j moles of J react with k moles of K to give m moles of M. If the reactants are modelled as ideal gases, we describe their activity, a as:
Activity:\(a = \)\({P \over {{P^0}}}\)
where P is the partial pressure of a reactant and P0 is standard pressure (0.1 MPa). Activity is linked to concentration in a similar way for dissolved reactants. The activities of reactants and products change the \(\Delta {\overline g _f}\) of the general reaction such that:
$$\Delta {\overline g _f} = \Delta {\overline g _f}^0 - RT\ln \left( {{{{a_J}^j \cdot {a_K}^k} \over {{a_M}^m}}} \right)$$
Which for a hydrogen fuel cell, H2 + ½O2 → H2O, becomes:
(10) \(\Delta {\overline g _f} = \Delta {\overline g _f}^0 - RT\ln \) \(\left( {{{{a_{{H_2}}} \cdot a_{{O_2}}^{{\textstyle{1 \over 2}}}} \over {{a_{{H_2}O}}}}} \right)\)
Note the trends: as product activity increases, \(\Delta {\overline g _f}\) decreases, i.e. less energy released. As reactant activity increases, \(\Delta {\overline g _f}\) increases hence more energy released. To see how this affects voltage we substitute equation (10) into equation (9) to get:
where E0 is the EMF at standard pressure. Equation (11) is an example of a Nernst equation. The EMF calculated using Nernst equations is called a Nernst Voltage and is the reversible cell voltage which would exist at a given temperature and pressure.
If, as an example, we took the temperature to be high such as that found in an SOFC, then the H2O could be modelled as an ideal gas meaning that equation (11) becomes:
$$E = {E^0} + {{RT} \over {2F}}\ln \left( {{{{{{P_{{H_2}}}} \over {{P^0}}} \cdot {{\left( {{{{P_{{O_2}}}} \over {{P^0}}}} \right)}^{{\textstyle{1 \over 2}}}}} \over {{{{P_{{H_2}O}}} \over {{P^0}}}}}} \right)$$
And if pressures are given in bar, then standard pressure P0 = 1, hence:
(12) $$E = {E^0} + {{RT} \over {2F}}\ln \left( {{{{P_{{H_2}}} \cdot P_{{O_2}}^{{\textstyle{1 \over 2}}}} \over {{P_{{H_2}O}}}}} \right)$$
This is a very useful equation.
Metal hydrides

A metal hydride tank (Image courtesy of ECD Ovonics)
A metal hydride cylinder, whilst technically a chemical method of storing the hydrogen, appears for all purposes to be just a hydrogen tank; hydrogen goes in and comes out unchanged. Some metals, usually alloys, have an affinity for hydrogen. The tanks are filled with finely divided grains of these alloys. The most common metals used are alloys of nickel, magnesium, iron, titanium, manganese, or chromium (or others). Different alloys offer different H2 capacities and dissociation characteristics. The metal grains essentially act as a hydrogen sponge, and need no reformers or fuel processors to supply a pure and consistent stream of H2. As seen in the table above, in terms of specific energy (amount of H2 per kilo) the technology doesn’t seem particularly beneficial. A figure of 0.58 kWhr per kg isn’t very large. However, when we consider the energy density (or H2 per unit volume) of the metal hydride, we find that it is even higher than cryogenic or high-pressure hydrogen.
The hydride tank would need to be filled at about 3 bar, which isn’t a dangerously high pressure. If the container was to leak, the temperature would fall and hinder the release of the gas further, hence it’s quite safe. The tank would only take a few minutes to fill.
The capacities of some different alloys are outlined below:
Alloy |
Moles of H stored per cm3 |
% of weight which is stored H |
MgH2 |
0.65 |
7.6 |
Mg2NiH4 |
0.59 |
3.6 |
FeTiH2 |
0.6 |
1.89 |
LaNi5H6 |
0.55 |
1.37 |
The only significant disadvantage of the technique is the mass of alloy required to store the H2; it’s quite heavy. These tanks are ideally suited for applications where space is at a premium but weight is not important. For example, in a boat some weight in the keel is an advantage to maintain stability but space is very limited. Another potential application is fuel cell powered electronics such as laptops.
In short, metal hydrides are a very promising technology.
Academic consultant: Derek Fray (University of Cambridge)
Content development: Áron Varga, Steve Mounsey
Web development: Jin Chong Tan
This DoITPoMS TLP was funded by the UK Centre for Materials Education and the Department of Materials Science and Metallurgy, University of Cambridge.


