Biaxial tension
The relationship between the entropy change and the extension can be simplified for biaxial tension of a sphere in much the same way as has already been seen for uniaxial tension. Consider a square piece of membrane, with initial unstretched side L0.
For biaxial tension:
λ1 = λ2, and λ1λ2λ3 = 1
therefore:
\[{\lambda _3} = \frac{1}{{\lambda _1^2}} = \frac{1}{{\lambda _2^2}} = \frac{1}{{{\lambda ^2}}}\]
putting this into the equation relating entropy change to extension ratios:
\[\Delta S = - \frac{1}{2}Nk\left( {\lambda _1^2 + \lambda _2^2 + \lambda _3^2 - 3} \right)\]
\[\Delta S = - \frac{1}{2}Nk\left( {2{\lambda ^2} + \frac{1}{{{\lambda ^4}}} - 3} \right)\]
From this, the work done per unit volume on stretching is:
\[w = \frac{1}{2}NkT\left( {2{\lambda ^2} + \frac{1}{{{\lambda ^4}}} - 3} \right) \;\;\;\;\;\;\;\;\;\;\; (1)\]
The work done on the square membrane is then the work done per unit volume multiplied by the area of the piece of membrane, L02, and the thickness, t0:
\[W = \frac{1}{2}NkT\left( {2{\lambda ^2} + \frac{1}{{{\lambda ^4}}} - 3} \right){t_0}L_0^2 \;\;\;\;\;\;\;\;\;\;\; (2)\]
If we now make an incremental change to the extension ratio, δλ, the amount of work needed to make this incremental extension is:
\[\delta W = 2F\left( {{L_0}\delta \lambda } \right)\;\;\;\;\;\;\;\;\;\;\; (3)\]
where F is the force and L0δλ is the change in extension. By re-arrangement of (3) it follows that:
\[F = \frac{1}{2}\left( {\frac{{\delta W}}{{\delta \lambda }}} \right)\left( {\frac{1}{{{L_0}}}} \right)\;\;\;\;\;\;\;\;\;\;\; (4)\]
Therefore, from (4) and (2):
\[F = NkT\left( {4\lambda - \frac{4}{{{\lambda ^5}}}} \right){t_0}\frac{{{L_0}}}{4}\;\;\;\;\;\;\;\;\;\;\; (5)\]
Rearranging (5), the force per unit length is given by:
\[\left( {\frac{F}{{\lambda {L_0}}}} \right) = NkT\left( {1 - \frac{1}{{{\lambda ^6}}}} \right){t_0} \;\;\;\;\;\;\;\;\;\;\; (6)\]
The total force acting over a cross sectional area of a sphere is given by Pπ2, where P is the internal pressure: this must be equal to the force per unit length acting around the circumference
\[NkT\left( {1 - \frac{1}{{{\lambda ^6}}}} \right){t_0}2\pi r = P\pi {r^2}\;\;\;\;\;\;\;\;\;\;\; (7)\]
from which, using the relationship that \(\lambda = \frac{r}{{{r_0}}}\), we have:
\[P = 2NkT\left( {{\lambda ^{ - 1}} - {\lambda ^{ - 7}}} \right)\left( {\frac{{{t_0}}}{{{r_0}}}} \right)\]
which gives us the predicted variation of pressure with increasing λ:
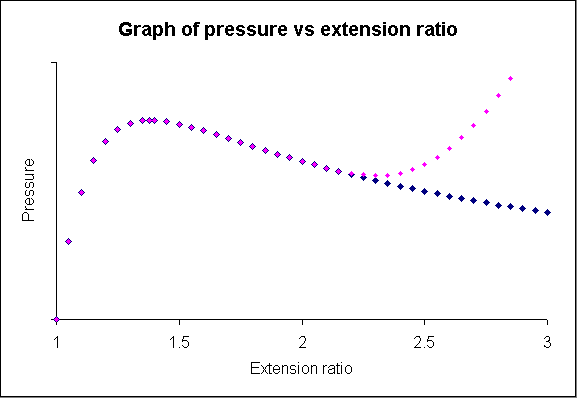
Graph of pressure vs extension ratio
This predicts that there will be a maximum value of pressure at an extension ratio of about 1.38, i.e. this is when the stiffness is a maximum. At high extension ratios (>2.5) however, the finite extensibility effect becomes apparent and the pressure becomes larger than predicted.

