Contraction of rubber

As was shown earlier in this TLP, the entropy change of an elastomer when it is stretched is given by:

\[\Delta S = - \frac{1}{2}Nk(\lambda _1^2 + \lambda _3^2 + \lambda _3^2 - 3)\]

This can be simplified when the shape change is uniaxial extension, when the extension ratios in the transverse directions must be equal:

λ₁ = λ₂

since there is no volume change, λ₁λ₂λ₃ = 1, and hence

\[{\lambda _1} = {\lambda _2} = \frac{1}{{\sqrt {{\lambda _3}} }}\]

Therefore:

\[\Delta S = - \frac{1}{2}Nk\left( {\frac{2}{{{\lambda _3}}} + \lambda _3^2 - 3} \right)\]

From

F = -T (dS/dL)

we have

\[F = \frac{{kTN}}{{{L_0}}}\left( {{\lambda _3} - \frac{1}{{\lambda _3^2}}} \right)\]

This leads to an expression for the nominal tensile stress:

\[\sigma = \frac{F}{{{A_0}}} = \frac{{kTN}}{{{V_0}}}\left( {{\lambda _3} - \frac{1}{{\lambda _3^2}}} \right)\]

Experimental data fits this theory well, except at high extensions when the chains reach maximum extension, causing the stiffness (gradient of plot) to increase greatly.

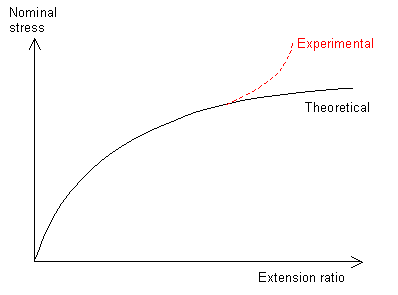
Graph of stress vs extension

It is therefore possible to estimate the chain segment density of a rubber, if the extension under a particular load is known. An example of such a calculation is given below:

Worked Example Calculation

A mass of 0.2 kg is suspended from a piece of rubber. The rubber is initially 10 cm long and has a circular cross section, of radius 2 mm. When the system equilibrates after the mass is attached, the new length of the rubber is 20 cm. The experiment is done at 298 K. Calculate the chain segment density in the rubber.

Solution

The equation we need is:

\[\sigma = \frac{F}{{{A_0}}} = \frac{{kTN}}{{{V_0}}}\left( {{\lambda _3} - \frac{1}{{\lambda _3^2}}} \right)\]

The cross-link density is N/V_o. Rearranging the above equation gives us:

\[\frac{N}{{{V_0}}} = F/{A_0}kT\left( {{\lambda _3} - \frac{1}{{\lambda _3^2}}} \right)\]

We can now calculate the force and cross-sectional area:

F = m g = 0.2 x 9.81 = 1.962 N

A₀ = πr² = π x (0.002)² = 1.26 x 10^-5 m²

Putting these values into our starting equation gives:

\[\frac{N}{{{V_0}}} = \frac{{1.962{\rm{N}}}}{{1.26 \times {{10}^{ - 5}}{{\rm{m}}^2} \times 1.38 \times {{10}^{ - 23}}{\rm{J}}{{\rm{K}}^{ - 1}} \times 298{\rm{K}} \times \left( {\frac{{0.2}}{{0.1}} - {{\left( {\frac{{0.1}}{{0.2}}} \right)}^2}} \right)}} = 2.17 \times {10^{25}}{{\rm{m}}^{ - 3}}\]

Therefore there are 2.17 × 10²⁵ chain segments per m³.