The Stiffness of Rubber (all content)
Note: DoITPoMS Teaching and Learning Packages are intended to be used interactively at a computer! This print-friendly version of the TLP is provided for convenience, but does not display all the content of the TLP. For example, any video clips and answers to questions are missing. The formatting (page breaks, etc) of the printed version is unpredictable and highly dependent on your browser.
Contents
Main pages
Additional pages
Aims
On completion of this TLP you should:
- Be able to predict the stiffness of rubber from a simple picture of its molecular structure
- Be able to use the stiffness to predict how rubber specimens of different shapes will deform
- Understand why rubber is known as an "entropy spring"
- Appreciate that the stiffness of rubber rises with increasing temperature, in contrast to all other materials
- Understand the pressure-size relationship exhibited by a balloon
Introduction
Rubbers (or elastomers) are polymers whose properties are affected by cross-linking between the individual chains. They have a fairly low cross-link density, with links at random intervals, usually of between 500 and 1000 monomers. These few cross-links are sufficient to prevent the unrestricted flow of whole molecules past neighbouring ones, but the chain segments between cross-links are free to move (provided the temperature is above the glass transition temperature, Tg). In particular, the segments can uncoil and recoil.
Statistical theory is able to provide mathematical relationships between the density of cross-links and measurable physical properties, such as the stiffness. These relationships can be used to predict the extension under a particular load, for example a balloon being inflated or a bungee jumper, or a measured property can be used to calculate the extent of cross-linking.
It is commonly known that most things get bigger when heated. Probably the best known example of a material that does not always expand when heated is water, but this only contracts on heating as the temperature rises from 0°C to 4°C. Outside this range it behaves as any other material. The explanation for the anomalous behaviour lies in a re-arrangement of the molecular structure. The underlying tendency for inter-atomic bond lengths to increase with rising temperature, which is due to the asymmetrical shape of the energy-spacing relationship, is common to all materials.
More on the energy-spacing relationship
Although rubber under normal conditions expands like other materials as it is heated, when under tension it behaves differently, contracting in the loading direction, rather than expanding, as it is heated. The explanation of this behaviour lies in the crucial contribution of entropy to the elasticity of rubber, which will be covered later in this package. It will also become clear why the stiffness of rubber is so much lower than other materials. Basically, this is because rubbers deform elastically by uncoiling of long, convoluted molecules, rather than by stretching of individual inter-atomic bonds.
Theory of rubber conformation
Polymer Coils
Polymer molecules are made up of many smaller units called monomers. A rubber is a fully amorphous, lightly cross-linked polymer, above Tg. They are normally composed of a -C-C- backbone chain. The bond angle is fixed at 109.5°, but the torsion angle can change, allowing the macroscopic shape of the chain to vary from being linear to being highly coiled and convoluted.
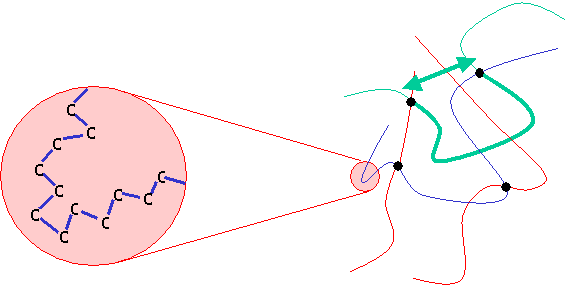
In this diagram, on the left each blue line represents a C-C link. The arrow shows the end-to-end distance of the chain segment, depicted as a thickened line. The segments tend to coil up to some extent, rather than aligning in a straight line. This can be thought of as the system increasing its entropy. The probability distribution for the end-to-end distance can be described mathematically by a Gaussian function:
\[P\left( {{{\vec r}_1},........,{{\vec r}_N}} \right) = {\left\{ {\frac{3}{{2\pi {b^2}}}} \right\}^{3N/2}}\exp \left\{ { - \sum\limits_{i = 1}^N {\frac{3}{{2{b^2}}}r_i^2} } \right\}\]
Tangles and Crosslinks
A piece of rubber, such as a rubber ball or a rubber band, is made up of many polymer molecules. As the molecules prefer to be coiled to a certain degree, rather than stretched out, the polymer molecules easily get tangled together. When chains become entangled, their mobility decreases. Furthermore, the entanglements mean that the chains cannot stretch as far as otherwise they would be able to and so the stiffness of the rubber increases - at least if it is measured over short timescales, which do not permit the entanglements to slide.
As well as physical entanglements, the chains can join together in another manner. If the chemistry of the chain is suitable, an atom belonging to one chain can form a chemical bond with an atom from another chain. This bond is called a cross-link. The nature of the cross-linking bonds is covalent. The cross-links inhibit the motion of the polymer chains and so increase the stiffness of the rubber. These are now stable over long time scales, so the stiffness is not time-dependent.
Coiling and Uncoiling
Consider what happens when you stretch a rubber band or a balloon. We know that the rubber will stretch a long way before it breaks, but we ought to be able to explain why it behaves the way it does.
When you first put the rubber under tension, the polymer molecules will begin to change their conformation. Pulling on the chains makes the polymers uncoil. This is shown schematically below:
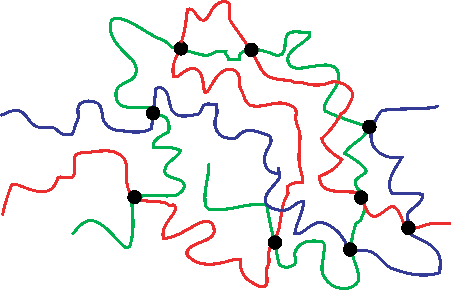
Unloaded coiled chains
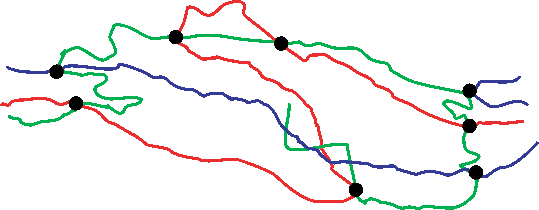
Loaded in tension
As you continue to pull on the rubber, the chain segments start to reach their limits of extensibility. In the case of silly putty or chewing gum, this sliding can continue until the chains no longer make contact and the rubber gets drawn out to a very thin cross section and perhaps fractures.
For conventional cross-linked rubbers, on the other hand, the chain segments uncoil as far as they can before the cross-links inhibit further uncoiling. Further tension now pulls directly on the C-C bonds of the polymer backbone. When the force becomes great enough, the C-C bonds will break and the rubber will snap. The strength of the rubber is thus not very different from other materials, whereas the stiffness is lower by orders of magnitude.
We should now be able to predict the shape of the extension vs force graph when extending rubber. This will be done for both uniaxial and biaxial tension later in the TLP.
Effect of sun on rubber band
Have you ever noticed what happens to a rubber band when it is left out in the sunshine for too long? The rubber becomes brittle and can break in your hand. The explanation for why this happens concerns cross-linking bonds.
Ultra-violet light from the sun provides the polymer molecules with the activation energy they need to be able to form more cross-links with other chains. When the rubber band is left out for a long time, the density of cross-links increases. When you try and stretch the rubber band, the chains are prevented from uncoiling or sliding past each other, due to the large number of cross-links. Because of this you are effectively pulling on the C-C backbone bonds of the polymer, which are very stiff and will not stretch much. Instead the rubber band snaps with very little extension.
Some oils and other chemicals have a similar effect on rubbers. However, butyl rubbers have a much lower density of available cross-link sites than other rubbers. Because of this it is much more difficult to form excess cross-link bonds and so butyl rubbers are resistant to degradation from U.V. light and from oils.
Thermodynamics - the entropy spring
When a stress is applied to a sample of cross-linked rubber, equilibrium is established fairly rapidly. Once at equilibrium, the properties of the rubber can be described by thermodynamics.
Consider an element of rubber placed under uniaxial tension. The first law of thermodynamics states that
dU = dQ - dW
where dU is the change in the system's internal energy, and dQ and dW are the heat and work exchanged between system and surroundings as the system undergoes differential change.
We are going to look at the specific case of uniaxial tension. Work done is given by force multiplied by distance, so the work done by a uniaxial force f is given by
dWf = –f dL
where dL is the differential change in the system's length due to the force f. (The negative sign implies that the work is done on the system).
If the deformation process is assumed to occur reversibly (in a thermodynamic sense), then
dQ = TdS
where S is the system's entropy. Combining the above equations gives (for uniaxial tension with V and T constant)
dU = TdS + f dL.
From this, the tensile (retractive) force
F = (dU/dL)T,V - T(dS/dL)T,V
The first term on the RHS is the energy contribution to the tensile (retractive) force, or energy elasticity. In rubbers, this represents the storage of energy resulting from rotation about bonds and the straining of bond angles and lengths from equilibrium values. The second term on the RHS is the entropy contribution to the tensile (retractive) force, or entropy elasticity. It is caused by the decrease in entropy upon uncoiling of the chain segments.
When rubber is extended, the change in length (and energy) comes almost entirely from a change in conformation, i.e. the rotation of bonds, and there is negligible stretching of the bonds. Therefore, at constant temperature, it can be approximated that the internal energy of the bonds does not change.
dU = 0
F = -T(dS/dL)
As the rubber is stretched, the chain is moving from a more probable (higher entropy) to a less probable (lower entropy) state. It is this lowering of entropy of the conformation that causes the retractive force, so rubber is described as an entropy spring.
Entropy derivation
It is possible to treat quantitatively the entropy change on extending a polymer chain:
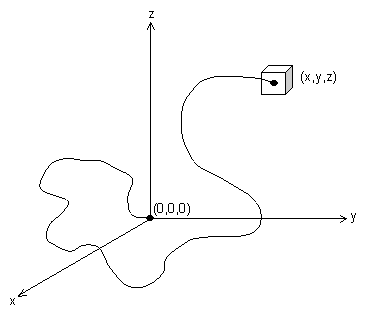
If one end of the chain is at (0,0,0), then the probability of the other end being at point (x,y,z) is:
\[p\left( {x,y,z} \right).dx.dy.dz = {\left( {\frac{b}{{\sqrt \pi }}} \right)^3}\exp \left[ { - {b^2}\left( {{x^2} + {y^2} + {z^2}} \right)} \right].dx.dy.dz\]
where
\[b = \sqrt {\frac{3}{{2n{a^2}}}} \]
a = bond length
n = number of links
If we stretch the chain, so that the end is at a new location (x',y',z') such that (x'2 + y'2 + z'2) > (x2 + y2 + z2), then p(x,y,z) will decrease, leading to a decrease in entropy. The entropy is given by
S = k lnΩ
where Ω = total number of possible conformations leading to the same end position. Now
Ω = p(x,y,z,)
On stretching a chain, so that the initial end point (x,y,z) changes to (x',y',z') where
x' = λxx
y' = λyy
z' = λzz
the associated change in entropy is given by
\[\Delta S = k\ln \left( {\frac{{\Omega '}}{\Omega }} \right) = k\ln \left( {\frac{{p'}}{p}} \right)\]
ΔS = −kb2 [((x')2 − x2) + ((y')2 − y2) + ((z')2 −z2)]
ΔS = −kb2 [(λx2 − 1) x2 + (λy2− 1)y2 + (λz2 − 1)z2]
In the unstressed state, with overall length r, we expect no preferential direction, so:
\[\left\langle {{x^2}} \right\rangle = \left\langle {{y^2}} \right\rangle = \left\langle {{x^2}} \right\rangle = \frac{{\left\langle {{r^2}} \right\rangle }}{3}\]
So, on average:
\[\Delta S = - k\left( {\frac{3}{{2n{a^2}}}} \right).\frac{{\left\langle {{r^2}} \right\rangle }}{3}.\left( {\lambda _x^2 + \lambda _y^2 + \lambda _z^2 - 3} \right)\]
From random walk theory,
〈 r2 〉 = na2
The entropy of a single chain segment can be multiplied by N (the no of chain segments) to give the total entropy change:
\[\Delta {S_{{\rm{tot}}}} = - \frac{1}{2}Nk\left( {\lambda _x^2 + \lambda _y^2 + \lambda _z^2 - 3} \right)\]
Contraction of rubber
As was shown earlier in this TLP, the entropy change of an elastomer when it is stretched is given by:
\[\Delta S = - \frac{1}{2}Nk(\lambda _1^2 + \lambda _3^2 + \lambda _3^2 - 3)\]
This can be simplified when the shape change is uniaxial extension, when the extension ratios in the transverse directions must be equal:
λ1 = λ2
since there is no volume change, λ1λ2λ3 = 1, and hence
\[{\lambda _1} = {\lambda _2} = \frac{1}{{\sqrt {{\lambda _3}} }}\]
Therefore:
\[\Delta S = - \frac{1}{2}Nk\left( {\frac{2}{{{\lambda _3}}} + \lambda _3^2 - 3} \right)\]
From
F = -T (dS/dL)
we have
\[F = \frac{{kTN}}{{{L_0}}}\left( {{\lambda _3} - \frac{1}{{\lambda _3^2}}} \right)\]
This leads to an expression for the nominal tensile stress:
\[\sigma = \frac{F}{{{A_0}}} = \frac{{kTN}}{{{V_0}}}\left( {{\lambda _3} - \frac{1}{{\lambda _3^2}}} \right)\]
Experimental data fits this theory well, except at high extensions when the chains reach maximum extension, causing the stiffness (gradient of plot) to increase greatly.
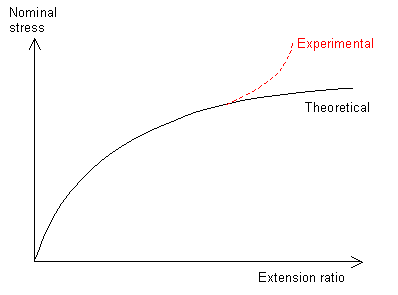
Graph of stress vs extension
It is therefore possible to estimate the chain segment density of a rubber, if the extension under a particular load is known. An example of such a calculation is given below:
Worked Example Calculation
A mass of 0.2 kg is suspended from a piece of rubber. The rubber is initially 10 cm long and has a circular cross section, of radius 2 mm. When the system equilibrates after the mass is attached, the new length of the rubber is 20 cm. The experiment is done at 298 K. Calculate the chain segment density in the rubber.
Solution
The equation we need is:
\[\sigma = \frac{F}{{{A_0}}} = \frac{{kTN}}{{{V_0}}}\left( {{\lambda _3} - \frac{1}{{\lambda _3^2}}} \right)\]
The cross-link density is N/Vo. Rearranging the above equation gives us:
\[\frac{N}{{{V_0}}} = F/{A_0}kT\left( {{\lambda _3} - \frac{1}{{\lambda _3^2}}} \right)\]
We can now calculate the force and cross-sectional area:
F = m g = 0.2 x 9.81 = 1.962 N
A0 = πr2 = π x (0.002)2 = 1.26 x 10-5 m2
Putting these values into our starting equation gives:
\[\frac{N}{{{V_0}}} = \frac{{1.962{\rm{N}}}}{{1.26 \times {{10}^{ - 5}}{{\rm{m}}^2} \times 1.38 \times {{10}^{ - 23}}{\rm{J}}{{\rm{K}}^{ - 1}} \times 298{\rm{K}} \times \left( {\frac{{0.2}}{{0.1}} - {{\left( {\frac{{0.1}}{{0.2}}} \right)}^2}} \right)}} = 2.17 \times {10^{25}}{{\rm{m}}^{ - 3}}\]
Therefore there are 2.17 × 1025 chain segments per m3.
Contraction experiment
The theory predicts that the stiffness of rubber is proportional to the temperature.
\[\sigma = \frac{{kTN}}{{{V_0}}}\left( {{\lambda _3} - \frac{1}{{\lambda _3^2}}} \right)\]
The result of this is that, if the rubber is extended under a fixed load, it is likely to contract when it is heated (even after allowance is made for the thermal expansion).
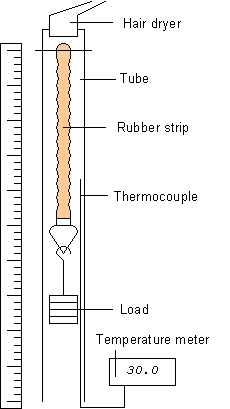
This can be observed using the following apparatus:
|
Diagram of apparatus |
In the demonstration, a rubber strip is suspended inside a vertical Perspex tube, alongside a metre rule. The rubber strip is stretched by attaching a small load to the bottom end. The rubber is then heated using a hair dryer directed into the top end of the tube. A thermocouple is positioned inside the tube and connected to a digital meter that gives the temperature in degrees Celsius (which must be converted to K for use in the equations).
In order to verify the theoretical explanation, you will need to make five observations from the demonstration:
- initial unloaded length of rubber strip (L0)
- loaded but unheated length of the rubber strip (L1)
- initial temperature (T1)
- loaded heated length of the rubber strip (L2)
- final temperature (T2)
Video of the contraction demonstration
Verification
The theoretical equation derived earlier relating extension and temperature was
\[\sigma = \frac{F}{{{A_0}}} = \frac{{kTN}}{{{V_0}}}\left( {\lambda - \frac{1}{{{\lambda ^2}}}} \right)\]
(The subscript has been dropped from λ since we are only considering one direction.) In the demonstration, F, A0, V0, N and k are all constant (once the load has been attached). Therefore, in order to verify this equation we need to show that
\[\frac{{{T_1}}}{{{T_2}}} = \left[ {{\lambda _2} - \frac{1}{{\lambda _2^2}}/{\lambda _1} - \frac{1}{{\lambda _1^2}}} \right]\]
where the subscripts 1 and 2 refer to before and after the contraction respectively, not different directions as in the earlier derivation. The following observations were made:
- Before the experiment began it was noted that the top of the rubber band was 0.96 m from the base of the metre rule.
- It was also noted that the length of the weights was 0.13 m.
- The length of the rubber strip when unloaded, L0, was 0.205 m.
These values will be used in our calculation to calculate the final length of the rubber strip. Using the recorded observations we have
\[\frac{{{T_1}}}{{{T_2}}} = \frac{{296}}{{338}} = 0.876\]
From the video of the readings before and after heating
\({\lambda _1}\) = \(\frac{{{L_1}}}{{{L_0}}}\) = \(\frac{{\left( {0.96 - 0.077 - 0.13} \right)}}{{\left( {0.205} \right)}}\) = 3.673, so \({\lambda _1} - \frac{1}{{\lambda _1^2}} = 3.599\)
\({\lambda _1}\) = \(\frac{{{L_1}}}{{{L_0}}}\) = \(\frac{{\left( {0.96 - 0.154 - 0.13} \right)}}{{\left( {0.205} \right)}}\) = 3.298, so \({\lambda _2} - \frac{1}{{\lambda _2^2}} = 3.206\)
Therefore
\[\left[ {{\lambda _2} - \frac{1}{{\lambda _2^2}}/{\lambda _1} - \frac{1}{{\lambda _1^2}}} \right] = \frac{{3.206}}{{3.599}} = 0.891\]
So, to a close approximation,
\[\left[ {{\lambda _2} - \frac{1}{{\lambda _2^2}}/{\lambda _1} - \frac{1}{{\lambda _1^2}}} \right] = \frac {{T_1}}{{T_2}} \]
and the theoretical explanation is verified. The small discrepancy is attributed to conventional thermal expansion; rubbers have relatively high expansivities (~ 50 x 10-6 K-1), so a rise in T of about 50 K will increase the length of a strip which is initially 0.75 m long by 2 mm.
Biaxial tension
The relationship between the entropy change and the extension can be simplified for biaxial tension of a sphere in much the same way as has already been seen for uniaxial tension. Consider a square piece of membrane, with initial unstretched side L0.
For biaxial tension:
λ1 = λ2, and λ1λ2λ3 = 1
therefore:
\[{\lambda _3} = \frac{1}{{\lambda _1^2}} = \frac{1}{{\lambda _2^2}} = \frac{1}{{{\lambda ^2}}}\]
putting this into the equation relating entropy change to extension ratios:
\[\Delta S = - \frac{1}{2}Nk\left( {\lambda _1^2 + \lambda _2^2 + \lambda _3^2 - 3} \right)\]
\[\Delta S = - \frac{1}{2}Nk\left( {2{\lambda ^2} + \frac{1}{{{\lambda ^4}}} - 3} \right)\]
From this, the work done per unit volume on stretching is:
\[w = \frac{1}{2}NkT\left( {2{\lambda ^2} + \frac{1}{{{\lambda ^4}}} - 3} \right) \;\;\;\;\;\;\;\;\;\;\; (1)\]
The work done on the square membrane is then the work done per unit volume multiplied by the area of the piece of membrane, L02, and the thickness, t0:
\[W = \frac{1}{2}NkT\left( {2{\lambda ^2} + \frac{1}{{{\lambda ^4}}} - 3} \right){t_0}L_0^2 \;\;\;\;\;\;\;\;\;\;\; (2)\]
If we now make an incremental change to the extension ratio, δλ, the amount of work needed to make this incremental extension is:
\[\delta W = 2F\left( {{L_0}\delta \lambda } \right)\;\;\;\;\;\;\;\;\;\;\; (3)\]
where F is the force and L0δλ is the change in extension. By re-arrangement of (3) it follows that:
\[F = \frac{1}{2}\left( {\frac{{\delta W}}{{\delta \lambda }}} \right)\left( {\frac{1}{{{L_0}}}} \right)\;\;\;\;\;\;\;\;\;\;\; (4)\]
Therefore, from (4) and (2):
\[F = NkT\left( {4\lambda - \frac{4}{{{\lambda ^5}}}} \right){t_0}\frac{{{L_0}}}{4}\;\;\;\;\;\;\;\;\;\;\; (5)\]
Rearranging (5), the force per unit length is given by:
\[\left( {\frac{F}{{\lambda {L_0}}}} \right) = NkT\left( {1 - \frac{1}{{{\lambda ^6}}}} \right){t_0} \;\;\;\;\;\;\;\;\;\;\; (6)\]
The total force acting over a cross sectional area of a sphere is given by Pπ2, where P is the internal pressure: this must be equal to the force per unit length acting around the circumference
\[NkT\left( {1 - \frac{1}{{{\lambda ^6}}}} \right){t_0}2\pi r = P\pi {r^2}\;\;\;\;\;\;\;\;\;\;\; (7)\]
from which, using the relationship that \(\lambda = \frac{r}{{{r_0}}}\), we have:
\[P = 2NkT\left( {{\lambda ^{ - 1}} - {\lambda ^{ - 7}}} \right)\left( {\frac{{{t_0}}}{{{r_0}}}} \right)\]
which gives us the predicted variation of pressure with increasing λ:
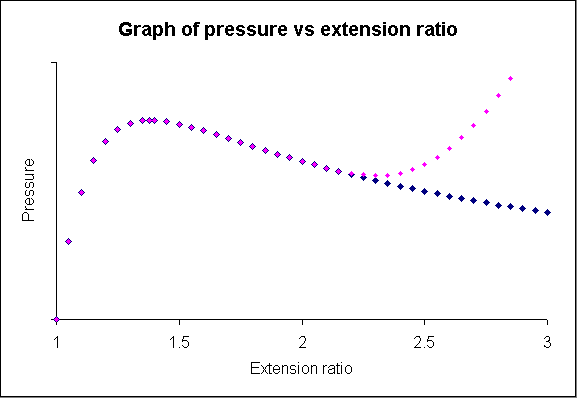
Graph of pressure vs extension ratio
This predicts that there will be a maximum value of pressure at an extension ratio of about 1.38, i.e. this is when the stiffness is a maximum. At high extension ratios (>2.5) however, the finite extensibility effect becomes apparent and the pressure becomes larger than predicted.
Balloon experiment
The biaxial theory can be tested using the apparatus shown.
Apparatus for the balloon experiment (Click on image to view larger version)
The data can also be used to estimate the volume density of chain segments, N. The balloon is not completely spherical, especially at smaller extensions, but the shape of the graph should be as predicted.
Method
Initially the balloon is completely filled, using a bicycle pump, while the bung is placed in the end of the U-tube, in order to make sure the coloured water does not spill out of the manometer. Once the balloon is fully inflated, the tap is closed, so that air cannot escape from the balloon, and the bung is removed in order to allow the trapped air out and the internal pressures to equalise.
The balloon radius is estimated, using calipers to measure the diameter in three orthogonal directions. Also, the height difference between the two menisci in the manometer is measured. Once these two values have been measured, a small amount of air is released from the balloon by opening the tap. The balloon reduces in size and the measurements are repeated until the balloon is at atmospheric pressure.
Analysis
The height difference can be related to the pressure inside the balloon by the equation:
P = ρ g h
where:
P = pressure inside the balloon
ρ = density of the liquid (water =
1 g cm-3)
g = acceleration due to gravity
h = height difference
To estimate the value of N, it is necessary to measure the initial thickness of the rubber, t0, and initial radius, r0. At Pmax, λ is approximately 1.38, so:
\[{P_{\max }} \approx 2NkT\left( {{{1.38}^{ - 1}} - {{1.38}^{ - 7}}} \right)\left( {\frac{{{t_0}}}{{{r_0}}}} \right)\]
\[{P_{\max }} \approx 1.24NkT\left( {\frac{{{t_0}}}{{{r_0}}}} \right)\]
\[N \approx \frac{{{P_{\max }}}}{{1.24kT}}.\frac{{{r_0}}}{{{t_0}}}\]
Results
The experiment was run three times, and the results are plotted on the following graph.
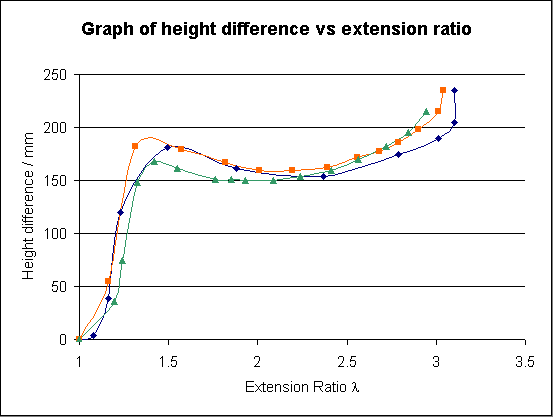
Below there is a series of photographs of the balloon and corresponding graphs.
Image sequence showing growth of pressure vs extension ratio graph ... in separate window
It can be seen that there is indeed a peak value of the pressure at an extension ratio of around 1.4. This "pressure barrier" to inflation at a low extension ratio is familiar to anyone who has tried to blow up a balloon by mouth.
It may be noted that some stiffening at high extension ratio might result from strain-induced crystallisation, but the predominant effect, at least for moderate values of λ, is thought to be that of non-Gaussian statistics.
Summary
In this teaching and learning package you have been familiarised with the following concepts:
- Polymer chains in rubbers are coiled up in their equilibrium state.
- When a rubber is stretched, this occurs by uncoiling of individual chain segments. Its stiffness is thus much lower than other materials, for which stretching occurs by lengthening of the inter-atomic bonds.
- The retractive force exerted by a stretched piece of rubber arises from the tendency of individual chain segments to recoil back to their equilibrium shape, thus raising the entropy and reducing the free energy. It is thus possible to predict the stiffness of a rubber solely from a knowledge of its crosslink density (which dictates the chain segment length).
You should also have read and understood the entropy spring derivation and be familiar with the idea that the retractive force a rubber exhibits under tension is caused by the lowering of the rubber's conformational entropy.
You should have seen how rubber deforms under uniaxial tension, observed the effect of heating a strip of rubber under tension and be able to explain both.
You should also have observed how a rubber membrane deforms under biaxial tension and be able to explain the three regimes
Questions
Quick questions
You should be able to answer these questions without too much difficulty after studying this TLP. If not, then you should go through it again!
-
Materials expand when heated because:
-
When rubber is put under uniaxial tension it:
-
Rubber differs from all other materials in that:
-
Approximately how many monomers are there in between cross-links in rubber?
-
What is meant by a change of conformation:
-
If a load is suspended from a rubber strip at room temperature, and the temperature is then reduced by 20°C, the load will be:
-
If a rubber strip is laid on a bench, unstretched at room temperature, and the temperature is then reduced by 20°C the strip will:
Deeper questions
The following questions require some thought and reaching the answer may require you to think beyond the contents of this TLP.
-
A bungee jumper, Bill, whose mass is 82.5 kg prepares to do a bungee jump. The bridge from which he will jump is 130 m high. The jumper understands why rubber behaves the way it does under tension because he has read the DoITPoMS TLP "Stiffness of Rubber". He asks the instructor what the dimensions of the bungee cord are and is told it is 60 m long when not stretched and has an initial diameter of 10 cm. Immediately after his successful jump he hangs stationary 20 m from the ground waiting to be pulled up again. While dangling there he estimates the cross-link density of the rubber. What should his answer be?
-
Explain why the bungee jumping cord should be made from butyl rubber (especially if it is to be used in a sunny country). You should explain what might happen if butyl rubber is not used and why this occurs.
-
Explain how the stiffness of a rubber membrane changes when it is put under biaxial tension, paying special attention to the three separate regimes of behaviour and explaining how each one occurs. Why do rubber bands snap when over-stretched whereas Silly Putty flows and necks until it separates into two pieces?
Open-ended questions
The following questions are not provided with answers, but intended to provide food for thought and points for further discussion with other students and teachers.
-
Can rubber be used as a structural material? Give examples of cases where it would be suitable.
-
You should now understand the way rubber behaves in uniaxial tension and the effect of temperature on its behaviour. Using what you have learnt consider how a large block of rubber would deform under uniaxial compression. You should use what you know about the way polymer chains behave in your answer.
-
Look back over the balloon experiment, where the deformation of rubber under biaxial tension was demonstrated. What do you think would happen if the balloon had been heated in the same way the rubber strip was heated in the first experiment? Would the balloon have contracted? What would have been the effect of heating the air inside the balloon?
Going further
Websites
- Bouncing Balls
"Everything you ever wanted to know about rubber (history, biographies, chemistry and conservation)", a site maintained by John Loadman. - Mongabay.com
"A Brief History of Rubber" (based on Wade Davis, One River 1996), a site maintained by Rhett A. Butler, promoting awareness of environmental issues surrounding rainforests. - International
Rubber Research and Development Board
"History of Natural Rubber", a site maintained by IRRDB, Kuala Lumpur, Malaysia.
The Lennard-Jones potential
The expansion of materials as their temperature is increased can be explained on a molecular level by the increased average spacing between atoms or molecules as they vibrate with greater amplitude at higher temperatures. This can be shown from the graph of potential energy against bond length, the Lennard-Jones potential.
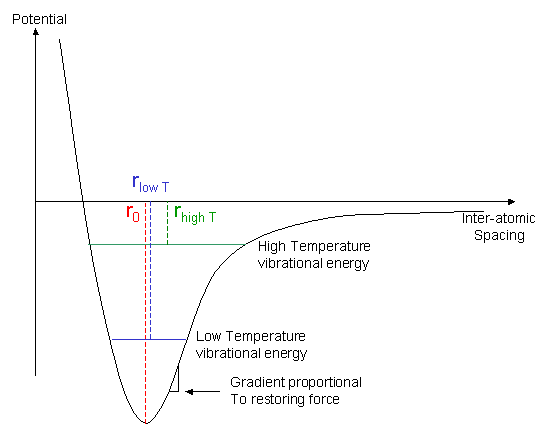
In the graph, r0 is the equilibrium bond length, i.e. the bond length when there is no atomic vibration, and r is the average bond length at an elevated temperature.
As the temperature is increased, the thermal energy available to the material increases, so the average vibrational energy of the bonds increases. It can be seen from the asymmetric form of the graph that this increase in energy will cause an increase in the average bond length. Under normal circumstances, this will cause the material to expand.
Furthermore, the plot illustrates why stiffness normally falls with increasing temperature. When a bond is stretched by an external load, the restoring force (tending to return the average bond length to its equilibrium value) is proportional to the gradient of this energy-separation curve. At high temperatures (vibration amplitudes), this restoring force is, on average, lower than at low temperatures.
Academic consultant: Bill Clyne (University of Cambridge)
Content development: Simon Adelman and Mark Wharton
Photography and video: Brian Barber and Carol Best
Web development: Dave Hudson
This TLP was prepared when DoITPoMS was funded by the Higher Education Funding Council for England (HEFCE) and the Department for Employment and Learning (DEL) under the Fund for the Development of Teaching and Learning (FDTL). Additional support for the development of this TLP came from the Armourers and Brasiers' Company and Alcan.