Effect of constraints

In the equations on the previous page, it was assumed that the surface energies of the two phases are identical, so that they have no effect in the energy balance, but this is not the case. The size of the crystal must be included in the driving force which is shown below.

\[ \Delta {U^{\text{t} \to \text{m}}} = \frac{4}{3}\pi {r^3}\Delta G + 4\pi {r^2}\Delta \gamma \]

where \( \Delta U \) is the total free energy change in units of joules (J), \( r \) is the radius of the monoclinic crystal produced, assumed here to be spherical, and \( \Delta \gamma \) is the difference in surface energies in J m⁻² of the monoclinic and tetragonal phases.

\( \Delta S \) remains unchanged. If we define the equilibrium transformation temperature in the absence of constraint to be \( T_ \text{e} \), \( \Delta H = T_ \text{e} \Delta S \). Therefore, at a temperature \( T \) below \( T_ \text{e} \), \( \Delta G = (T_ \text{e} - T) \Delta S \).

Setting \( \Delta {U^{\text{t} \to \text{m}}} \) to be zero, because martensitic transformations are spontaneous and do not require a classical nucleation and growth approach to analyse their transformation like liquid → solid and other solid → solid phase transformations, we find that

\[ \frac{4}{3}(T_\text{e}-T) \pi{r^3}\Delta S^{{\text{t} \to \text{m}}} + 4\pi {r^2}\Delta \gamma = 0 \]

This defines a lower temperature, \( T = T' \) for the transformation of a particle of size \( r \) to transform, where

so that, in words, the temperature at which a tetragonal zirconia particle will transform spontaneously to being a monoclinic zirconia particle is determined by its size.

Hence, if the zirconia particles are embedded in an untransforming matrix such as alumina, and if there is no constraint by the surrounding matrix (which we examine below), then on cooling below the equilibrium transformation temperature to (say) room temperature, we can predict that large tetragonal particles will transform, but small particles will not.

For the martensitic transformation in zirconia, \( T_ \text{e} \) is 1240 °C, \( \Delta \gamma \) is 3 J m⁻² and \( \Delta S \) = −120 kJ m⁻³ K⁻¹, so that for \( T' \) to be room temperature (20 °C), \( r \) is 61.5 nm. Therefore, without considering constraint, it can be deduced that only very small particles would remain untransformed at room temperature.

In a real physical situation, the situation is even more complex. The equation above is for a single crystal transforming in a matrix which we assume does not apply any constraint. In practice, there will be elastic constraint from this matrix which will inhibit the martensitic transformation. This will manifest itself in an additional strain energy term in the energy balance:

\[\Delta {U_E} = \frac{1}{6}k{\theta ^2}V\]

where \( V \) is the volume, \( \theta \) is the volumetric strain, ⅙ is just a geometric factor and \( k \) is a function of the elastic constants given by:

\[ k = 2\frac{{{E_\text{M}}{E_\text{p}}}}{{{E_\text{M}} + {E_\text{p}}}} \]

where \( E_\text{M} \) is the stiffness of the matrix and \( E_\text{p} \) is the stiffness of the particle. This further shifts the line to the left in the graph shown in the animation further down the page.

As before, \( \Delta S \) remains unchanged. The spontaneous transformation \( T'' \) for a particle of size \( r \) is now:

\[ T'' = T_\text{e} - \left| \frac{3 \Delta \gamma}{r \Delta S} \right| - \left| \frac{k \theta^2}{6 \Delta S} \right| \]

Therefore, the effect of strain energy is to make the spontaneous transformation of particles of a particular size less likely.

Transformation energy

If sufficient stress is applied at room temperature to an untransformed tetragonal particle which has been prevented from transforming because of its size and the degree of volumetric strain, the transformation to the monoclinic phase can occur.

The work required for this is seen in the graph above. Using the difference between \( T'' \) and \( T \) with the gradient

\[ \Delta W = - {f}\Delta {S}\left( {{T} - {T''}} \right) \]

• Stress must act to reduce the misfit of the transformation, because there is a volume expansion when going from the tetragonal form of zirconia to the monoclinic form
• The hydrostatic component of the stress (the component of the stress tensor associated with a change in volume, i.e., the dilatational component) must be tensile.

Cracks have high stresses at the tip. If the far field stress is tensile, then the crack tip must also have a hydrostatic tensile stress, \(\sigma_\text{H}\). Using tensors in a uniaxial set up:

\[ {\sigma_\text{H}} = \frac{1}{3}{\rm{\;}}{\sigma_0}{\rm{\;\;\;\;\;\;\;\;\;\;for\;a\;stress\;tensor\;\;\;\;}}\left( {\begin{array}{*{20}{c}}
{{\sigma _0}}&0&0\\
0&0&0\\
0&0&0
\end{array}} \right) \]

or, in terms of strain, if there is a volumetric (hydrostatic) strain \( \theta \), the linear strain along a particular axis is

\[ \varepsilon = \frac{1}{3}\;\theta \]

Therefore, the work, \( \Delta W \), associated with the dilatational component of the martensitic phase transformation for a volume fraction of particles, \( f \), is

\[ \Delta W = f{\sigma_\text{H}}\theta = f{\sigma_0}\varepsilon \]

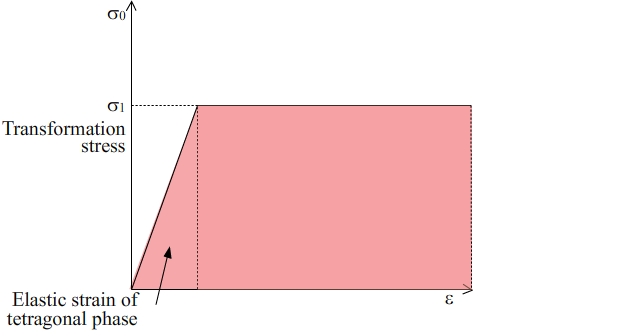
Figure 3: Uniaxial Stress - linear strain graph of the transformation from the tetragonal phase to the monoclinic phase in zirconia. The area shaded in pink is the energy absorbed. The elastic strain energy contribution of the tetragonal phase is small relative to the work done in causing the martensitic transformation of this phase to the monoclinic phase

Hence, for an applied uniaxial stress \( \sigma_{\text{t}} \) where the critical linear strain is \( \varepsilon_{\text{t}} \) (so that the volumetric strain is \( 3\varepsilon_{\text{t}} \)), particles which would have transformed spontaneously at \( T'' \) will now transform at a temperature \( T \) defined by the relationship

\[ {\sigma_\text{t}} = - \frac{{\Delta S\left( {T - T''} \right)}}{{{\varepsilon_\text{t}}}} \]

This applied uniaxial stress will act to toughen the material if the martensitic transformation is not reversible on removal of the stress, so that the work per unit volume put into the material is absorbed by the material.

Contribution to fracture resistance

If the far field stress is insufficient to cause the tetragonal to monoclinic phase transformation, then only a local region near the crack tip will transform. The size of the transformed zone can be calculated by working out the stress distribution ahead of the crack tip which is given by:

\[ \sigma \left( r \right) = \frac{K}{{\sqrt {2\pi r} }} \]

where \( K \) is the stress intensity factor and \( r \) is the distance from the crack tip. For a sharp surface crack of length \( a \) and an applied stress, \( \sigma_\text{app}, K = 1.12\sigma_\text{app}\sqrt{\pi a} \). For other situations, 1.12 is replaced by a more general geometric factor, \( Y, \) dependent on the specific situation.

We can rearrange the equation for the size of the transformed zone to show that when the transformation stress, \( \sigma_\text{t} \), has been reached in the vicinity of the crack tip, the size of the transformation zone, \( r_\text{t} \), is given by an expression of the form

\[ {r_\text{t}} = A{\left( {\frac{K}{{{\sigma_\text{t}}}}} \right)^2} \]

where \( A \) is a geometric constant.

If we take this distance to be the extent of the transformation either side of the crack plane, then for a unit area of crack plane the work done in causing the martensitic transformation, \( \Delta {\Gamma_\text{t}} \), will produce the extra resistance to fracture:

\[ \Delta {\Gamma_\text{t}} = 2{r_\text{t}} f {\sigma_\text{t}}{\varepsilon_\text{t}} \]

Assuming that \( f \) remains constant and recognising that \( \varepsilon_\text{t} \) is a constant, it follows that

\[ \Delta {\Gamma_\text{t}} \propto \frac{{{\sigma_\text{t}}}}{{\sigma_\text{t}^2}} = \frac{1}{{{\sigma_\text{t}}}} \]

Therefore, the lower the transformation stress required, \( \sigma_\text{t} \), the larger the degree of resistance is to fracture, and therefore, the more tough is the material.