Crack deflection criterion derivation
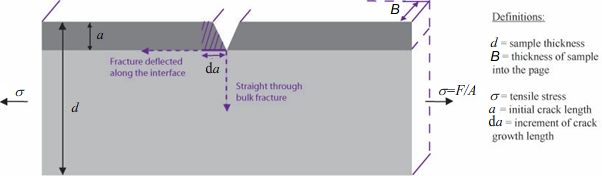
The interface has fracture resistance, \( \Gamma_\text{i} \), whereas the bulk has a fracture resistance of \( \Gamma_\text{bulk} \).
For simplicity, we will assume the stiffness of the two layers is the same and consider the changing surface energies and strain energies to determine whether the crack deflects along the interface or propagates through the bulk.
Consider the increment of crack growth of length \( {\rm{d}}a \) along the interface. This results in two energy changes: the interface is broken to form two surfaces, increasing the surface energy which opposes crack growth, together with a relaxation of the thin layer of material which favours crack growth.
The increment of surface energy is given by:
\[ {\rm{d}}{U_S} = {{\rm{\Gamma }}_\text{i}}B{\rm{d}}a \]
This assumes that the surface energy is the main contribution to the fracture resistance.
If we assume that the thin layer was constrained to have the same strain as the thick layer when it was bonded the release in stain energy will be:
\[ {\rm{d}}{U_E} = \; - \frac{1}{2}E{\varepsilon ^2}Ba{\rm{d}}a \]
where \( E \) is the common Young's modulus of each layer and \( \varepsilon \) is the strain to which the system is being subjected. Before the crack deflects, the main strain in the block, \( \varepsilon \), is:
\[ \varepsilon = \frac{\sigma }{E} = \frac{F}{{BdE}} \]
so that
\[ {\rm{d}}{U_E} = \; - \frac{1}{2}E{\left( {\frac{F}{{BdE}}} \right)^2}Ba{\rm{d}}a = \; - \frac{{{F^2}a}}{{2EB{d^2}}}{\rm{d}}a \]
The rate of change of the total energy, \( U \), with crack length increment, \( {\rm{d}}a \), is given by the equation
\[ \frac{{{\rm{d}}U}}{{{\rm{d}}a}} = \;\frac{{{\rm{d}}{U_S}}}{{{\rm{d}}a}} + \frac{{{\rm{d}}{U_E}}}{{{\rm{d}}a}} \]
By substitution
\[ \frac{{{\rm{d}}U}}{{{\rm{d}}a}} = {{\rm{\Gamma }}_\text{i}}B - \frac{{{F^2}a}}{{2EB{d^2}}} \]
The condition for interfacial cracking to begin is then
\[ \frac{{{\rm{d}}U}}{{{\rm{d}}a}} = 0 \]
Hence the applied force \( F \) at which this occurs is given by the expression
\[ F = Bd\sqrt {\frac{{2E{{\rm{\Gamma }}_\text{i}}}}{a}} \]
By comparison, the Griffith criterion for crack growth through the bulk can be given as:
\[ {F_{bulk}} = Bd\sqrt {\frac{{E{{\rm{\Gamma }}_\text{bulk}}}}{{\pi a}}} \]
For crack deflection, we clearly want \( F < F_\text{bulk} \). Therefore, the criterion for crack deflection can be given as:
\[ \frac{{{{\rm{\Gamma }}_\text{i}}}}{{{{\rm{\Gamma }}_\text{bulk}}}} < \frac{1}{{2\pi }} \]
Composite materials with suitably low values of interfacial fracture resistance will therefore be able to use crack deflection as their main toughening mechanism to increase the total path length, and therefore increase the work of fracture.

