Dissemination of IT for the Promotion of Materials Science (DoITPoMS)

DoITPoMS Teaching & Learning Packages Ternary Phase Diagrams Applying the Gibbs phase rule to ternary systems
Ternary Phase Diagrams AimsBefore you startIntroductionRepresenting ternary phase diagramsSections through ternary phase diagramsTie lines and tie trianglesApplying the Gibbs phase rule to ternary systemsSolidification of ternary alloys – complete solid solutionSolidification of ternary alloys – one eutectic valleySolidification of ternary alloys – Class I reactionsSolidification of ternary alloys – Class II reactionsSolidification of ternary alloys – Class III reactionsCase Study: Sn-Ag-Cu systemUses of ternary alloysSummaryQuestionsGoing further
TLP creditsTLP contentsShow all content
Viewing and downloading resourcesAbout the TLPsTerms of useFeedbackCredits Print this page
PreviousNext

Applying the Gibbs phase rule to ternary systems

In a ternary system the number of components is three, c = 3. The total number of degrees of freedom (the number of variables - composition variable, temperature or pressure - that must be specified to define the state of a system) and phases (homogenous regions of the system) is five.

As ternary systems are often considered as temperature-composition diagrams, pressure is fixed. This reduces the number of degrees of freedom by one.

For a constant pressure (or equally a constant temperature), the total number of degrees of freedom and phases in a ternary system is four.

There can be:

  • One phase and three degrees of freedom
  • Two phases and two degrees of freedom
  • Three phases and one degree of freedom
  • Four phases and no degrees of freedom

Consider a system with a ternary eutectic reaction:

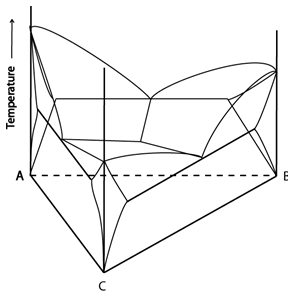
Figure 6: A space model for a ternary system with a ternary eutectic point. Adapted from https://commons.wikimedia.org/wiki/File:Space_diagram_of_a_three-component_system.jpg

Single Phase Regions

Single phase regions are volumes where the alloy can lie on any point in the volume.

Single phase regions have three degrees of freedom. They are trivariant equilibria.

This means that to define the equilibrium (the point in ternary space the alloy lies on), three variables must be specified and that three variables can be altered without moving out of the single-phase region.

Temperature and the proportion of two of the endmembers must be specified to define the position of the alloy.

Temperature and the proportion of two of the endmembers (which implicitly alters the proportion of the third endmember – see Representing Ternary Phase Diagrams for more about defining a ternary composition) can be varied without leaving the single-phase region.

Two Phase Regions

Two phase regions are volumes. They can be considered as a stack of isothermal sections; the edges of these sections define the surfaces bounding the two-phase region. Each isothermal section contains a stack of tie lines which span the area. An alloy can lie on any tie line in the volume.

Two phase regions have two degrees of freedom. They are bivariant equilibria.

To define which tie line the alloy lies on, a temperature and the proportion of one component in one of the two phases must be specified or two composition variables can be specified (the proportion of two components in one of the two phases or the proportion of a component in each phase).

Once the tie line is specified, the temperature and the composition of both phases can be found, and the state of the system is defined.

Three Phase Regions

Three phase regions are volumes. They can be thought of as a stack of isothermal tie triangles (each corner of the triangle gives the composition of a phase – see Tie Lines and Tie Triangles for more information). The edges of these tie triangles define the surfaces bounding the three-phase region. An alloy can lie on any of these isothermal tie triangles.

Three phase regions have one degree of freedom. They are univariant (or monovariant) equilibria.

To define which tie triangle the alloy lies on, either the temperature or the proportion of one component in one of the constituent phases must be specified.

Four Phase Regions

Four phase equilibria have no degrees of freedom. They are invariant equilibria and are represented by points in ternary space at a fixed temperature and composition.

By specifying that four phases are in equilibrium, the state of the system is defined to be at the invariant point.

Changing any variables requires the system to move off this point and to cease being in a four-phase equilibrium.

Invariant Reactions

Reactions are often associated with heating and cooling through invariant points as there is a drastic change in the phases present across the point.

There are three main classes of ternary invariant reactions:

Class I – ternary eutectic reactions which are analogous to binary eutectic reactions. They have a generalised equation of:

\[ \rm{L \rightleftharpoons \alpha + \beta + \gamma} \]

Directly above the invariant point there is a single-phase region and directly below it there is a three-phase region.

Class II – this ternary invariant reaction has no direct binary equivalent. It is sometimes referred to as a peritectic type, but this can cause confusion with Class III reactions. To avoid confusion, this type of reaction is sometimes called an ubergang reaction, from the German for ‘crossing’. They have a generalised equation of:

\[ \rm{L + \alpha \rightleftharpoons \beta + \gamma} \]

Directly above the invariant point there is a two-phase region and directly below it there is a different two-phase region.

Class III – ternary peritectic reactions which are analogous to binary peritectic reactions. They have a generalised equation of:

\[ \rm{L + \alpha + \beta \rightleftharpoons \gamma} \]

Directly above the invariant point there is a three-phase region and directly below it there is a single-phase region.

There is more information on each of these reactions on the pages about solidification of ternary alloys.

There are other kinds of ternary invariant reactions (for example solid state reactions and reactions involving gases) but they can all be placed into one of the three classes outlined above.

PreviousNext